Tensorflow

Posted on Edited on In Views: Word count in article: 1.3k Reading time ≈ 5 mins.
Tensorflow is a free and open-source software library for machine learning and artificial intelligence. It has a particular focus on training and inference of neural networks.

Basic data structure

See Numpy and Tensorflow.

Neural networks

Normalize data

Fitting the weights (w, b) to the data will proceed more quickly if the data is normalized. In tensorflow, we can use Normalization to normalize data. It uses z-score. However, it is a preprocessing layer rather than an independent layer of model.

1
2
3
4
from tensorflow.keras.layers import Normalization
norm_l = Normalization(axis=-1)
norm_l.adapt(X) # learns mean, variance
Xn = norm_l(X)
  • axis=-1 means that it will normalize the last dimension of X. For 2-D arrays, it will normalize the column. In this case, axis=-1 is equal to axis=1.
  • After normalizing, the test set should also be normalized: X_testn = norm_l(X_test).

Create the model

For a neural network like this:

1

Fig. 1. Sample

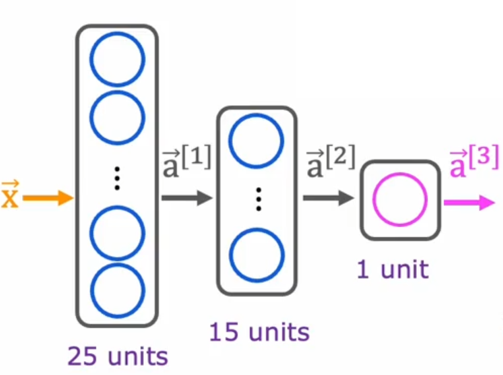
we can create the neural network using tensorflow in Python:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense

# non-regularization
model = Sequential([
    # We can use the following code to specify the shape of input layer
    ## tf.keras.Input(shape=(x,))
    Dense(units=25, activation='sigmoid'),
    Dense(units=15, activation='sigmoid'),
    Dense(units=1, activation='sigmoid')
                   ])
# regularization
model = Sequential([
    Dense(units=25, activation='sigmoid', kernel_regularizer=L2(0.01)),
    Dense(units=15, activation='sigmoid', kernel_regularizer=L2(0.01)),
    Dense(units=1, activation='sigmoid', kernel_regularizer=L2(0.01))
                   ])  # 0.01 is the value of lambda

Keras is an open-source software library that provides a Python interface for neural networks. It is now a package under tensorflow,which acts as an interface.

  • units represents the number of neuron in this layerr.
  • activation represents the activation function you choose for this layer.
  • Dense is a kind of hidden layer that make use of all the inputs for each neuron.
  • We can also assign names to each layer using name='xx'. For the first layer, using input_dim=xx is another way to specify the shape of input layer.
  • When specifying the shape of input layer, model will be instantiated. That is, parameters of all layers will be initialized.
  • Use .summary to get the structure of model. Use .get_layer('layer_name') to get the certain layer.

We can also create the neural network layer by layer:

1
2
3
4
5
6
7
8
9
10
import numpy as np

x = np.array([[10, 11]])
layer_1 = Dense(units=25, activation='sigmoid')
layer_2 = Dense(units=15, activation='sigmoid')
layer_3 = Dense(units=1, activation='sigmoid')

a1 = layer_1(x)
a2 = layer_2(a1)
a3 = layer_3(a2)  # the final output

For each layer, we can use .get_weights() to get its w and b. Feed some examples to instantiate them or use .set_weights([w, b]) to initialize them.

The first way is more convenient and universal, as it builds a neural network at once.

Name of activation functions in keras:

  • relu
  • sigmoid
  • linear
  • softmax
  • ...

Loss and cost functions

1
2
3
4
5
6
7
8
from tensorflow.keras import losses

# for binary classificaiton
model.compile(loss=losses.BinaryCrossentropy())
# for linear regression
model.compile(loss=losses.MeanSquaredError())
# for Adam algorithm
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3), loss=YourChoiceOfFunction)

See Adam algorithm to know more about Adam.

At this step, the structure of the neural network has already been established.

The name of some loss functions in losses:

  • BinaryCrossentropy: Binary classification
  • MeanSquaredError: Linear regression
  • SparseCategoricalCrossentropy: Multiclass classification

If we regard the whole neural network as a generalized model, the model and cost function can be represent as:
$$
f(W,B)(\vec{x})
$$
$$
J(W,B)=\frac{1}{m}\sum\limits_{i=1}^{m}L(f(\vec{x}^{(i)},y^{(i)}))
$$

Regularization

When regularization, we just need to add:

1
kernel_regularizer=tf.keras.regularizers.l2(0.1) # 0.1 is the value of lambda

to the layer that we want to regularize.

Gradient descent

This is the final step to train a neural network. In this step, we use gradient descent to determine $W$ and $B$.

Capital means matrix

1
model.fit(X, y, epochs=100)

The algorithm used in fit is called Backpropagation. X,y is our training set and epochs represents the number of iterations.

After finishing the training of neural network, we can use model.predict() or model() to predict or infer.

The type of model.predict() is tf while the type of model() is np.

Optimization for softmax

In multiclass classfication, the following code will work, but the value is not very accurate. See Softmax regression to know more about multiclass classification and softmax.

1
2
3
4
5
6
7
8
9
10
11
12
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy

model = Sequential([
    Dense(units=25, activation='relu')
    Dense(units=15, activation='relu')
    Dense(units=10, activation='softmax')
                   ])
model.compile(loss=SparseCategoricalCrossentropy())
model.fit(X, y, epochs=100)

Due to the limitations in precision when using binary to represent decimals, the more intermediate values we use, the greater the loss of precision we get. Before we calculate $loss$, we must get the value of $a$. $a$ is a intermediate value, so it is advisable for us to replace $a$ in $loss$ with its original formula. That is:
$$a_i=g(z)=\frac{e^{z_i}}{e^{z_1}+...+e^{z_i}}$$
$$loss=-\log{a_1}, y=1...$$
$$\downarrow$$
$$loss=-\log\frac{e^{z_i}}{e^{z_1}+...+e^{z_i}},y=1...$$
To realize this, we just need to set the activation function of output layer to linear and set from_logits to True:

1
2
3
4
5
6
model = Sequential([
    Dense(units=25, activation='relu')
    Dense(units=15, activation='relu')
    Dense(units=10, activation='linear')
                   ])
model.compile(loss=SparseCategoricalCrossentropy(from_logits=True))

The principle of this code is that $g(z)$ is just $z$, and tensorflow will replace $a$ with its original formula in loss function. from_logits actuallly means use $z$ rather than $a$. This gives tensorflow more flexibility to rearrange the terms to get more accurate values.

In this case, the output of our neural network is actually a vector of $z$. Therefore, we have to add 

1
2
logit = model(X)
f_x = tf.nn.softmax(logit)

to get the real values. However, to get the label, we just need to use np.argmax(y_pred, axis=0).

The same optimization can also be applied to other neural networks, like binary classification.

Regression model

For regression models, Auto Diff (Auto Grad) of Tensorflow can help us get partial derivatives automatically.

Gradient descent

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import tensorflow as tf
# for J = (wx-1)^2

w = tf.Variable(3.0) # The parameters we want to optimize, they can also be vector
x = 1.0 # Features of trainng set
y = 1.0 # Target value of training set
alpha = 0.01 # Learning rate

iterations = 30 # Number of iteration

for iter in range(iterations):
    with tf.GradientTape() as tape: # Record the steps
        fwb = w * x # Model
        costJ = (fwb - y)**2 # Cost function which should be implemented by ourselves
    [dJdw] = tape.gradient(costJ, [w]) # Calculate derivatives

    w.assign_add(-alpha * dJdw) # Update w

Adam algorithm

The example used here is about collaborative filtering. See Collaborative filtering to know more about it.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from tensorflow import keras

# Instantiate an adam optimizer
W = tf.Variable(tf.random.normal((num_users,  num_features),dtype=tf.float64),  name='W')
X = tf.Variable(tf.random.normal((num_items, num_features),dtype=tf.float64),  name='X')
b = tf.Variable(tf.random.normal((1,          num_users),   dtype=tf.float64),  name='b')

optimizer = keras.optimizers.Adam(learning_rate=1e-1)

iterations = 200
for iter in range(iterations):
    with tf.GradientTape() as tape:
        # features, w, b, mean normalization, R (which item have a rating), number of users, number of items, lambda
        coast_value = cofiCostFuncV(X, W, b, Ynorm, R, num_users, num_items, lambda) # Compute cost which should be implemented by ourselves
    grads = tape.gradient(cost_value, [X, W, b]) # Calculate derivatives
    optimizer.apply_gradients(zip(grads, [X, W, b])) # Update X, W, b

More information