Decision Trees

Structure of decision trees

Decision trees are a tree model, where each internal node (decision node) is a feature that has several possibile values. The number of values defines the degree of nodes.

Fig. 1. Decision trees

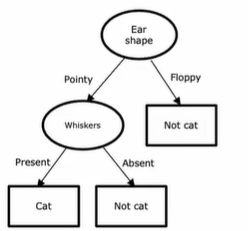
Decision tree learning

First decision: How to choose features to maximize purity? Second decision: When can the tree stop splitting

• When a node is 100% one class.
• When splitting a node will result in the tree exceeding a maximum depth (defined by us).
• When improvements in purity score are below a threshold.
• When number of examples in a node is below a threshold.

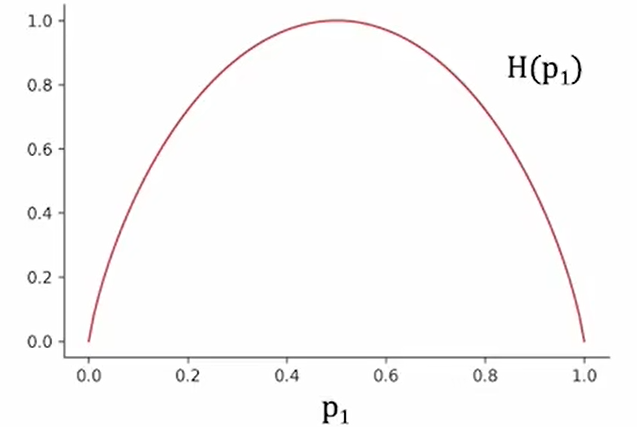
Measuring purity

p$_1$: Fraction of examples that are our target.

H(p$_1$): Degree of impurity of one set.

$$p_0=1-p_1$$
$$H(p_1)=-p_1\log_2(p_1)-p_0\log_2(p_0)$$

Fig. 2. Entropy function

Choosing a split

Information gain

Information gain is the redunction of entropy after one split:

$$IG=H(p_1^{root})-(w^{left}H(p_1^{left})+w^{right}H(p_1^{right}))$$

where $w^{left}H(p_1^{left})+w^{right}H(p_1^{right})$ is the average weighted entropy of two child nodes. $w$ is the propotion of examples in left/right node that come from root node.

Building a decision tree

We always construct decision trees in a preorder traversal. That is:

• Start with all examples at root node;
• Calculate information gain for all possible features and pick the one with the highest information gain;
• Split dataset and build subtrees recursively until stopping criteria is met.

For features with more than two discrete values, we can use one-hot encoding. That is, decompose the features with $k$ values into $k$ bool features so that the values of each new feature will only be yes (1) or no (0). One-hot encoding can also be applied to neural networks to turn multiclass classification to binary classification.

For features with continuous values, we try splitting values using different thresholds and choose the threshold that gives the highest information gain.

It is reasonable that the same features appears several times in one decision trees.

Regression trees

Regression trees are the generalization of decision trees, which predict a number. The differences between building a regression tree and a decision tree are:

• The prediction of regression trees is the average value of examples in leaf node;
• We choose the features to splite dataset by the reduction of variance.

For the second difference:

• Calculate the average weighted variance of one split:
  $$w^{left}v^{left}+w^{right}v^{right}$$
• Calcuate the reduction of variance after splitting:
  $$v^{root}-(w^{left}v^{left}+w^{right}v^{right})$$
• Choose the feature that gives the highest reduction and continue until meet stopping criteria.

Ensemble of decision trees

A single decision tree is highly sentitive to small changes of the data. We may get two totally different decision trees even though only one example changes in the training set. An ensemble of decision trees will make the overall algorithm more robust. An ensemble of decision trees makes decision by voting, that is, the prediction of the ensemble is the value most decision trees give.

Fig. 3. Ensemble of decision trees

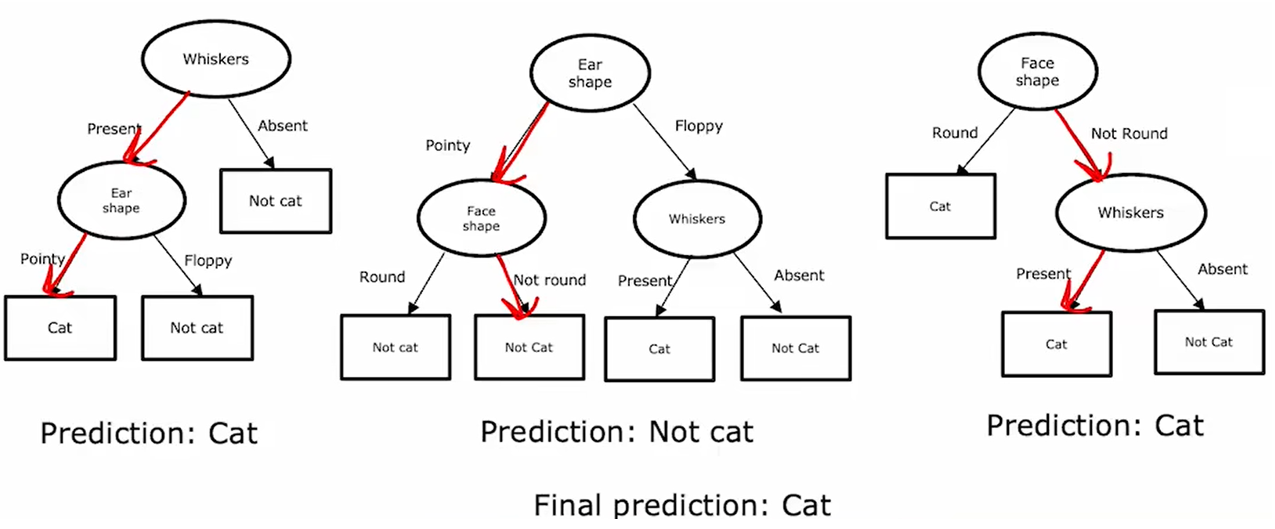
Random forest algorithm

One algorithm to create an ensemble of decision trees is random forest algorithm. The algorithm can automatically explore a lot of small changes to the data set, which makes it more robust.

Random forests are generated by sampling with replacement and randomizing feature choice:

• Determine the number of trees $B$ we need and the size of subset $m$;
• Use sampling with replacement to create a new training set of size $m$;
• Randomly pick a subset of $k$ (usually $\sqrt{n}$) features from $n$ features and train a decision tree only use these features and the data set generated above;
• Repeatedly generate $B$ trees.

Sampling with replacement and randomizing feature choice allow us generate different trees as much as possible.

XGBoost

XGBoost is an open-source library that makes ensemble of decision trees perform better. The core idea of XGBoost is that it is more worthwhile to train decision trees using the examples that the previously trained decision trees have failed to predict rather than using totally random examples. Trees generated like this is called boosted trees. In XGBoost, instead of picking subsets from all samples with equal probability, it makes it more likely to pick examples that the previously trained trees have misclassfied. The details of XGBoost are very complicated, but the using of it is quite simple:

from xgboost import XGBClassifier # or XGBRegressor for regression

model = XGBClassifier()

model.fit(X_train, Y_train)
y_pred = model.predict(X_test)

Decision trees & Neural Networks

For decision trees and tree ensembles:

• Work well on structured data; [advantage]
• Fast to train; [advantage]
• Small decision tress may be human interpretable; [advantage]
• Not recommended for unstructured data (images, audio, text) [disadvantage];
• Can't train multiple trees at a time. [disadvantage]

Neural Networks:

• Works well on all types of data; [advantage]
• Works with transfer learning; [advantage]
• Multiple neural networks can be easier to string together when building a system of multiple models working together; [advantage]
• Take long time to train. [disadvantage]