Model Selection & Hyperparameter Optimization

Evaluating a model

See Machine learning diagnostics to know the basic methods of evaluating a model.

When evaluating a model, we sometimes may not have enough data for cross validation. The method we use to solve this problem is K-fold Cross Validation.

K-fold Cross Validation

K-fold Cross Validation is a technique used for hyperparameter tuning such that the model with the most optimal value of hyperparameters can be trained in a rather small data set. The advantage of this approach is that each example is used for validation exactly once in each test fold and all examples will be used for validation finally. The following are steps in K-fold Cross Validation:

1. Split the dataset into training set and test set;
2. Split training set into K-folds;
3. Choose K-1 folds for training and 1 fold for validation;
4. Train the model with specific hyperparameters in K-1 folds and validate it using the 1 fold;
5. Record its performance;
6. Choose another K-1 folds for training and 1 fold for validation;
7. Repeat 4, 5, 6 until each of the K-fold get used for validation purpose;
8. Evaluate the mean performance of K models;
9. Step 3-8 for different hyperparameters; (optional)
10. Choose the hyperparameters which result in best performance; (optional)
11. Train the model using the whole training set.

Fig. 1. K-fold Cross Validation

In general, we seldom use K-fold since it is time-consuming. We often set K 5 or 10.

• K-Fold Cross Validation – Python Example

Model capacity and data

The model capacity is a model's ability to fit the function. It's very close for model complexity. High model capacity always means a deeper and larger neural network or more complex polynomials. Data or the complexity of data is determined by the size of dataset, the features number of each data, the diversity of samples, etc. Model capacity and data together determine the performance of a model:

Fig. 2. Model capacity and data

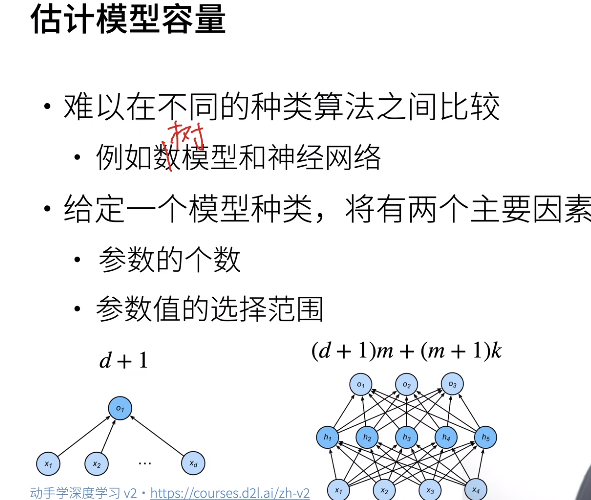
For neural networks, a simple way to evaluate model capacity is to compute the number of model parameters that the neural network can learn, or to evaluate the range of each parameter (w, b):

Fig. 3. Evaluating model capacity

VC dimension*

The VC dimension of a model is the maximum number of points that can be arranged so that shatters them. More formally, it is the maximum cardinal such that there exists a generally positioned data point set of cardinality can be shattered by. -- From Google

For a perceptron with inputs of N dimensions, its VC dimension is $N+1$ or $O(N\log_2N)$, that is, it can classify $N+1$ ($O(N\log_2N)$) points. VC dimension can be used to evaluate the model capacity though it doesn't work well.

Dropout

Dropout is another method of regularization besides weight decay. The motivation of dropout is that a good model should be robust to input perturbations. Dropout achieves this by adding noise to the ouptout of hidden layers:
$$
\text{dropout}[x]=x'
$$
where:
$$
x_i'=
\begin{cases}
0, &p \\
\frac{x_i}{1-p}, &1-p
\end{cases}
$$
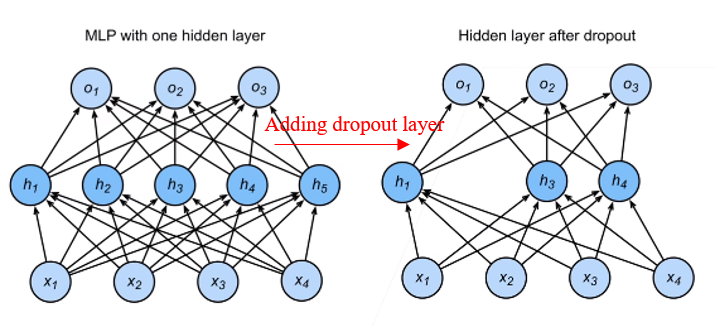
$p$ is a hyperparameter that controls the probability of dropout. Usually, we set $p$ to 0.1, 0.5 or 0.9. The meaning of the formula above is that dropout layer randomly sets the output of the neurons in a hidden layer to 0 (with probability $p$) or $\frac{1}{1-p}$ times as much as the origin value (with probability $1-p$). This works because when one value is set to 0, it is equivalent to remove a neuron from the hidden layer, which makes the neural network a sub neural network. Since dropout is totally random, we are actually training a model using multiple neural networks, which will make the model more robust.

Fig. 4. Dropout

To ensure the accuracy, we must make sure that the expectation of dropout is equivalent to its original value:
$$\text{E}[x']=x$$

Since dropout is a kind of regularization, it only works when training models. When making predictions, we don't use dropout layer, like weight decay.

In general, we use dropout in the dense layer of MLP.