Paper001: Dataset Condensation with Gradient Matching

Posted on Edited on In Views: Word count in article: 4k Reading time ≈ 15 mins.
这篇论文是对传统的数据蒸馏（Dataset Distillation）的一种改进，称“数据缩合”（Dataset Condensation）。这是数据蒸馏领域最具突破性的研究之一。该论文首次提出了梯度匹配策略，以该策略蒸馏出来的数据集的测试准确率和泛化精度都有了极大的提升。

数据蒸馏

当前最先进的深度学习技术几乎都采用的是大数据训练大模型的方式。这样的方式能够得到如GPT-4等具有远超我们想象的性能的大模型，但是其训练的算力和内存开销是一般人难以承担的。

数据蒸馏（Dataset Distillation）是解决这种问题的一种技术。它以学习的方式，从初始的大训练数据集（the original large training set）中（e.g. MNIST, CIFAR10等经典的数据集）获得一个更小的合成数据集（synthetic set）。这个合成数据集的数据量可能只有原数据集的1%，但是，用该数据集训练得到模型的性能可以达到用原数据集训练得到模型性能的80%~100%，同时也能具有不输于原模型的泛化性能。下图显示了数据蒸馏的目标。需要注意的是，原数据集与合成数据集训练的网络是一模一样的，测试集中的数据也是一模一样的，不同的只是训练集中的数据。

1

Fig. 1. Dataset Distillation

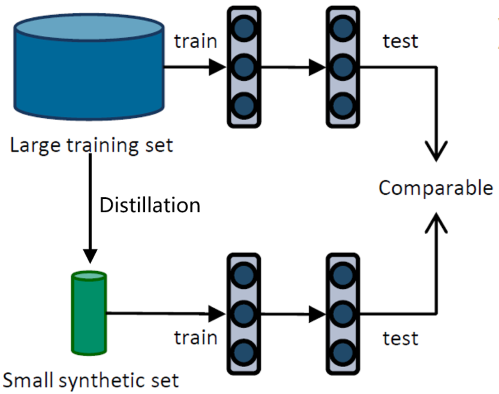
除了所用的训练集不同外，合成集训练得到的模型和原集得到的模型几乎一致（实际的模型参数可能不同）。因此，以后再用同样的数据集训练模型时，完全可以使用更小、训练速度更快的合成数据集，而测试和部署时模型的输入依旧为未经合成处理的数据。

2

Fig. 2. Process of dataset distillation

数据缩合

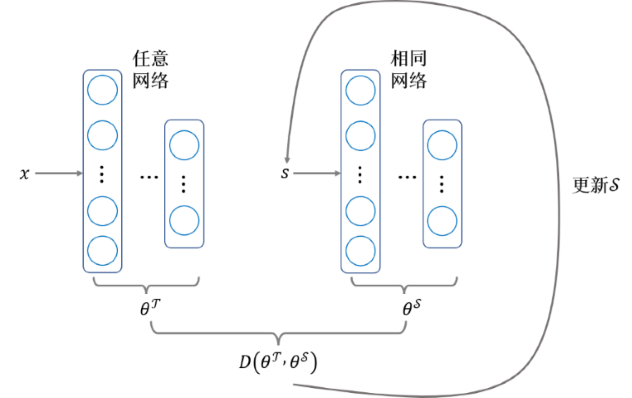
本篇论文发表于ICLR 2021，第一作者是Dr. Bo Zhao。论文中用到的数据蒸馏方法称“数据缩合”（Dataset Condensation）。其最基本的设想是：合成集模型要想获得可与原集模型相媲美的性能和泛化能力，只要两个集合训练出的模型具有相似的模型参数就好了，即：对于原数据集$\mathcal{T}=\left\{(x_i,y_i)\right\}| _{i=1} ^\mathcal{|T|}$，其中$x\in\mathbf{R}^d$，是单一样本的特征，$y\in\left\{0,1,...,C-1\right\}$，是单一样本的标签，$C$是类别个数；对于合成数据集$\mathcal{S}=\left\{(s_i,y_i)\right\}| _{i=1} ^\mathcal{|S|}$，其中$s\in\mathbf{R}^d$，是单一合成样本的特征，$y\in\left\{0,1,...,C-1\right\}$，是单一合成样本的标签，其类别和数量与原标签一致，它们分别独立训练相同网络的最优化模型参数分别为：

$$
\begin{align*}
\theta ^{\mathcal{T}}&=\arg\min _{\theta}\mathcal{L ^T}(\theta)\tag{1}\\
\theta ^{\mathcal{S}}&=\arg\min _{\theta}\mathcal{L ^S}(\theta)\tag{2}
\end{align*}
$$

其中，$\mathcal{L}$是代价函数（Cost Function），两个训练集采用相同的代价函数，而$\theta ^{\mathcal{T}}$和$\theta ^{\mathcal{S}}$则分别是网络达到最优状态时的模型参数，两者相似，即它们之间的距离要尽可能地小：

$$
\min _\mathcal{S}D(\theta ^{\mathcal{T}},\theta ^{\mathcal{S}})\quad \text{subject to} \quad \theta ^{\mathcal{S}}(\mathcal{S})=\arg\min _{\theta}\mathcal{L ^S}(\theta)\tag{3}
$$

其中$\theta ^{\mathcal{S}}$是$\mathcal{S}$的函数是因为我们期望找到这么一个合成集$\mathcal{S}$，使得由它训练得到的$\theta ^{\mathcal{S}}$能够满足$(3)$。训练开始时，我们一般会把$\theta ^{\mathcal{T}}$和$\theta ^{\mathcal{S}}$初始化为相同的值$\theta_0$，其中$\theta_0\sim P _{\theta_0}$。但是不同的$\theta_0$可能会得到不同的$\theta ^{\mathcal{T}}$，因此，更进一步地，我们希望不同$\theta_0$下距离的期望是最小的，于是$(3)$转变为：

$$
\min _\mathcal{S}\text{E} _{\theta_0\sim P _{\theta_0}} [D(\theta ^{\mathcal{T}} ({\theta_0}),\theta ^{\mathcal{S}} ({\theta_0}))]\quad \text{subject to} \quad \theta ^{\mathcal{S}}(\mathcal{S})=\arg\min _{\theta}\mathcal{L ^S}(\theta ({\theta_0})) \tag{4}
$$

一般情况下，给定$\theta_0$，$\theta ^{\mathcal{T}}$可以通过训练网络得到。此后，$\theta ^{\mathcal{T}}$便可用于训练$\mathcal{S}$，这包含两层的循环：

  1. 任意初始化一个$\mathcal{S}$集；
  2. 内层循环：根据给定的$\theta_0$和当前的$\mathcal{S}$，训练与$\theta ^{\mathcal{T}}$相同的网络，得到当前的$\theta ^{\mathcal{S}}$，此过程对应$(4)$的后一项；
  3. 外层循环：初始化内层循环的$\theta_0$，内层循环结束后，计算$\theta ^{\mathcal{T}}$和$\theta ^{\mathcal{S}}$之间的距离，得到梯度（$\mathcal{S}$为自变量），更新$\mathcal{S}$，此过程对应$(4)$的前一项。

3

Fig. 3. Process of dataset condensation

不难看出，每次内层循环都相当于重新训练了一个网络，这是很浪费算力的。然而在实际操作的过程中，我们并没有必要每次都训练出当前$\mathcal{S}$下最优的$\theta ^{\mathcal{S}}$，毕竟这只是个近似值。因此，实际上，我们采用用特定的优化算法优化了几步得到的$\theta ^{\mathcal{S}}$作为近似值即可，即：

$$
\theta ^{\mathcal{S}}(\mathcal{S})=\text{opt-alg} _{\theta}(\mathcal{L ^S}(\theta),\varsigma) \tag{5}
$$

其中$\varsigma$是优化（梯度下降）的次数，而$\text{opt-alg}$是任意的优化算法（e.g. adam, sgd, etc.），$\theta$是$\theta_0$的函数，此处为方便不写出，后面也是。

合成的是特征$\mathcal{s}$，不对labels进行合成操作。

梯度匹配

上面的数据缩合方法又称参数匹配法（Parameter Matching），即以让$\theta ^{\mathcal{S}}$逐渐逼近$\theta ^{\mathcal{T}}$的方式来训练得到$\mathcal{S}$。该方法有两个弊端：

  1. $\theta ^{\mathcal{T}}$与$\theta ^{\mathcal{S}}$之间可能相差很大且一个网络的模型参数空间很大，优化路径中可能存在若干局部最小值，因此难以达到最优解；
  2. 限定步数的$\text{opt-alg}$得到的参数过于不精确，但为了计算性能只能这么做。

最原始的数据蒸馏算法用的就是参数匹配法。数据蒸馏和数据缩合实际上是一回事，只不过数据缩合特指这篇文章所用到的蒸馏算法。

这篇论文提出的能解决上述问题的方法称梯度匹配（Gradient Matching），其核心思想在于：不仅让$\theta ^{\mathcal{T}}$和$\theta ^{\mathcal{S}}$最终的值相近，且遵循的优化路径也相近。于是式$(4)$就变成：

$$
\begin{align*}
\min _\mathcal{S}\text{E} _{\theta_0\sim P _{\theta_0}} [\sum\limits _{t=0} ^{T-1}D&(\theta _t ^{\mathcal{T}},\theta _t ^{\mathcal{S}})]\quad \text{subject to}\tag{6}\\
\theta ^{\mathcal{S}} _{t+1}(\mathcal{S})=\text{opt-alg} _{\theta}(\mathcal{L ^S}(\theta _t),\varsigma ^{\mathcal{S}}) \quad&\text{and}\quad \theta ^{\mathcal{T}} _{t+1}=\text{opt-alg} _{\theta}(\mathcal{L ^T}(\theta _t),\varsigma ^{\mathcal{T}})
\end{align*}
$$

其中$\varsigma ^{\mathcal{S}}$和$\varsigma ^{\mathcal{T}}$分别是$\mathcal{S}$和$\mathcal{T}$一次优化的梯度下降次数，$T$是迭代次数。整个式$(6)$表明，$\mathcal{S}$要使得整个迭代过程中的距离和最小，即$\mathcal{S}$要使得$\theta ^{\mathcal{T}}$与$\theta ^{\mathcal{S}}$几乎遵循相同的优化路径。每一次梯度下降，$\theta ^{\mathcal{T}}$与$\theta ^{\mathcal{S}}$的变化如下所示：

$$
\theta ^{\mathcal{S}} _{t+1} \leftarrow \theta ^{\mathcal{S}} _{t}-\eta_\theta\nabla_\theta \mathcal{L} ^{\mathcal{S}}(\theta _t ^{\mathcal{S}}) \quad\text{and}\quad \theta ^{\mathcal{T}} _{t+1} \leftarrow \theta ^{\mathcal{T}} _{t}-\eta_\theta\nabla_\theta \mathcal{L} ^{\mathcal{T}}(\theta _t ^{\mathcal{T}})\tag{7}
$$

其中$\eta_\theta$是学习率而其后续项为梯度。

4

Fig. 4. Dataset condensation with gradient matching

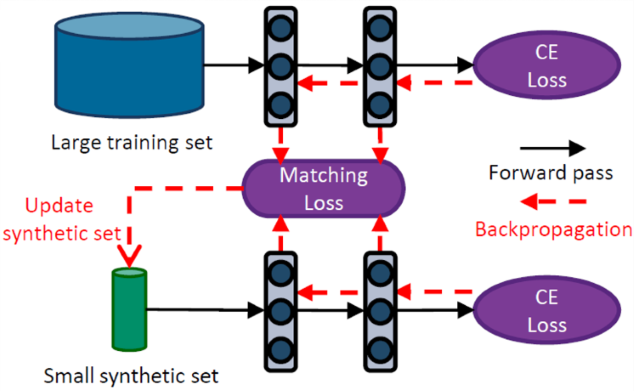
由于$\theta ^{\mathcal{T}}$与$\theta ^{\mathcal{S}}$均初始化为$\theta_0$，所以在计算距离$D(\theta _t ^{\mathcal{T}},\theta _t ^{\mathcal{S}})$时：

$$
\theta ^{\mathcal{S}} _{0}-\eta_\theta\nabla_\theta \mathcal{L} ^{\mathcal{S}}(\theta _0 ^{\mathcal{S}}) -(\theta ^{\mathcal{T}} _{0}-\eta_\theta\nabla_\theta \mathcal{L} ^{\mathcal{T}}(\theta _0 ^{\mathcal{T}}))=\eta_\theta\nabla_\theta \mathcal{L} ^{\mathcal{T}}(\theta _0 ^{\mathcal{T}})-\eta_\theta\nabla_\theta \mathcal{L} ^{\mathcal{S}}(\theta _0 ^{\mathcal{S}})\tag{8}
$$

因此，实际上我们只需要计算梯度的距离，并让其尽可能地小即可，于是式$(6)$又可转变为：

$$
\min _\mathcal{S}\text{E} _{\theta_0\sim P _{\theta_0}} [\sum\limits _{t=0} ^{T-1}D(\nabla_\theta \mathcal{L} ^{\mathcal{S}}(\theta _t ^{\mathcal{S}}),\nabla_\theta \mathcal{L} ^{\mathcal{T}}(\theta _t ^{\mathcal{T}}))] \tag{9}
$$

即，只要梯度下降的方向相近即可。

实际上，$\varsigma ^{\mathcal{S}}$和$\varsigma ^{\mathcal{T}}$由优化算法决定，不同的优化算法，在处理完所有训练数据后，梯度下降的次数不同。$\theta _t ^{\mathcal{T}}$和$\theta _t ^{\mathcal{S}}$实际上值相同，因为实际训练时分两个阶段：训练并更新$\mathcal{S}$和训练并更新$\theta_t$，而$\mathcal{S}$和$\mathcal{T}$经过的都是相同的网络，所以$\theta_t$也是一样的。$\theta_t$的梯度下降使用的数据是$\mathcal{S}$，这也在一定程度上造成了该方法的误差。

由于梯度是向量，而对于多参数的梯度下降，重要的是下降的方向，因此距离$D$采用两个向量的余弦距离，而不是欧式距离：

$$
\begin{align*}
D(\mathbf{A},\mathbf{B})
&=1-cos<\mathbf{A},\mathbf{B}>\\\
&=1-\frac{\mathbf{A}\cdot\mathbf{B}}{||\mathbf{A}||\space||\mathbf{B}||}\tag{10}
\end{align*}
$$

重要代码

以下只是对文中代码的简单实现（并不能运行），具体代码详见文章提供的开源部分Dataset Condensation。

5

Fig. 5. Pseudocode in paper

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
# 参数定义
num_exp = 5  # 重复实验次数
num_classes = 10  # 实验为图片分类，使用数据集MNIST，共10个类
ipc = 1  # 为每个类只训练一张合成图片
channel = 1  # 对黑白图片，输入通道为1
im_size = [28, 28]  # MNIST图片尺寸为28x28
device = torch.device('cuda')  # 用GPU训练
lr_img = 0.1  # 合成图片学习率
lr_net = 0.01  # 模型参数学习率
K = 1000  # 最外层循环，使得合成集S能适应模型参数的不同初始化方式
T = 1  # 里一层循环，对不同ipc有不同的值，相当于训练合成图片时的epoch，因为合成图片在一次循环中只对一个类更新一次
batch_real = 256  # 原训练集的批量大小
batch_train = 256  # 训练模型参数时的批量大小
inner_loop = 1  # 训练模型参数时的迭代次数

# 重复实验
for exp in range(num_exp):
    '''对原训练集和合成集的初始化'''
    # 一些获取训练集T的操作，最终得到的特征和标签依次为（MNIST）:
    # images_all: Tensor，shape (6000, 1, 28, 28)，其中6000为样本数，1为输入通道数（因为是黑白图片），28x28是图片像素
    # labels_all: Tensor，shape (6000)，6000为样本数，类别为10，包含0~9的手写数字

    # 可训练的合成图片，shape (10, 1, 28, 28)
    image_syn = torch.randn(size=(num_classes*ipc, channel, im_size[0], im_size[1]), dtype=torch.float32, requires_grad=True, device=device)
    # 不可训练的合成图片标签，shape (10)
    label_syn = torch.tensor([np.ones(ipc)*i for i in range(num_classes)], dtype=torch.long, requires_grad=False, device=device).view(-1)

    '''优化算法、损失函数'''
    # 对合成图片的优化算法为使用动量法的SGD
    optimizer_image = torch.optim.SGD([image_syn, ], lr=lr_img, momentum=0.5)
    optimizer_image.zero_grad()  # 梯度清零
    # 损失函数，因为梯度是原网络训练时模型参数产生的梯度，而本实验是个图片分类问题，因此使用的仍是softmax的损失函数
    criterion = torch.nn.CrossEntropyLoss().to(device)

    '''for k = 0, ... ,K - 1'''
    for k in range(K+1):
        # 源代码在此处存在在特定结点分析训练效果的代码，此处省略
        
        # 获取某个指定的网络同时随机初始化模型参数，原文存在参数，此处省略，仅作为示意
        net = get_network().to(device)
        net.train()  # 使网络进入训练模式
        net_parameters = list(net.parameters())
        # 优化模型参数的优化函数，采用简单的SGD
        optimizer_net = torch.optim.SGD(net.parameters(), lr=lr_net)
        optimizer_net.zero_grad()

        '''for t = 0, ... ,T - 1'''
        for t in range(T):
            # 此处还有对BatchNorm做的优化，也省略

            # 将所有类别的梯度差异相加再计算二阶混合偏导
            loss = torch.tensor(0.0).to(device)

            '''for c = 0, ... ,C - 1，训练合成图片'''
            # 对不同的类别单独训练
            for c in range(num_classes):
                # 从原训练集的c类中随机获取batch_real张图片，注意，get_images是原文定义的内联函数，因此可以直接访问images_all，而此时images_all已经被放到GPU中了
                img_real = get_images(c, batch_real)
                # lab_real是新数据，要先放入GPU
                lab_real = torch.ones((img_real.shape[0]), device=device, dtype=torch.long) * c
                # 同样地获取合成集中对应类别的数据
                img_syn = image_syn[c*ipc:(c+1)*ipc].reshape(ipc, channel, im_size[0], im_size[1])
                lab_syn = torch.ones((ipc), device=device, dtype=torch.long) * c

                '''数据过网络'''
                # 原训练集
                output_real = net(img_real)
                loss_real = criterion(output_real, lab_real)
                gw_real = torch.autograd.grad(loss_real, net_parameters)  # 获得原训练集的梯度
                gw_real = list((_.detach().clone() for _ in gw_real))  # 逐层处理且将梯度从计算图中分离

                output_syn = net(img_syn)
                loss_syn = criterion(output_syn, lab_syn)
                gw_syn = torch.autograd.grad(loss_syn, net_parameters, create_graph=True)  # 获得合成集的梯度，不过因为要计算二阶混合偏导，因此要保留计算图

                # 余弦距离
                def distance_wb(gwr, gws):
                    shape = gwr.shape
                    if len(shape) == 4:  # conv_layer: out*in*h*w
                        gwr =gwr.reshape(shape[0], shape[1]*shape[2]*shape[3])
                        gws =gws.reshape(shape[0], shape[1]*shape[2]*shape[3])
                    elif len(shape) == 3:  # layer_norm: C*h*w
                        gwr =gwr.reshape(shape[0], shape[1]*shape[2])
                        gws =gws.reshape(shape[0], shape[1]*shape[2])
                    elif len(shape) == 2:  # linear_layer:h*w
                        tmp = "do nothing"
                    else:  # only bias
                        gwr =gwr.reshape(1, shape[0])
                        gws =gws.reshape(1, shape[0])
                    # torch.norm: 默认求F范数，即矩阵各元素平方和开根号
                    # 此处实际上是先求每层每个神经元的余弦距离最后再将余弦距离相加（改变形状后，gwr和gws的第一维是神经元个数）
                    return torch.sum(1 - torch.sum(gwr*gws, dim=-1) / (torch.norm(gwr, dim=-1) * torch.norm(gws, dim=-1) + 0.000001))
                
                def match_loss(gw_syn, gw_real):
                    dis = torch.tensor(0.0).to(device)

                    for ig in range(len(gw_real)):
                        gwr = gw_real[ig]
                        gws = gw_syn[ig]
                        dis += distance_wb(gwr, gws)
                    
                    return dis

                loss += match_loss(gw_syn, gw_real)
            
            '''更新合成图片'''
            optimizer_img.zero_grad()  # 合成图片矩阵的梯度清零
            loss.backward()  # 计算对合成图片矩阵的二阶混合偏导
            optimizer_img.step()  # 梯度下降

            '''更新模型参数'''
            # 深拷贝，完全复制合成图片和label，防止在训练模型参数时合成图片生成计算图
            image_syn_train, label_syn_train = copy.deepcopy(image_syn.detach()), copy.deepcopy(label_syn.detach())
            # 小批量训练的迭代器
            dst_syn_train = TensorDataset(image_syn_train, label_syn_train)
            trainloader = torch.utils.data.DataLoader(dst_syn_train, batch_size=batch_train, shuffle=True, num_workers=0)
            # 我认为这一步正是DC的缺陷所在，合成集数据本身就已经不准了，用它更新的模型参数大概率偏离原来的方向
            for il in range(inner_loop):
                epoch(trainloader)  # 一次迭代：梯度下降、模型参数更新

实验设计

实验主要分为三个部分：

  1. 与现有核心集选择法和数据蒸馏法的性能比较；
  2. 缩合数据的泛化性分析；
  3. 缩合数据的数量与性能分析。

采用的数据集分别为MNIST，SVHN，FashionMNIST和CIFAR10，网络结构有六种：MLP，ConvNet，LeNet，AlexNet，VGG-11和ResNet-18。每种结构5次重复实验，在训练$\mathcal{S}$的过程中，当k达到一定次数时，会用$S$去训练20个随机初始化的网络以分析训练效果。

与现有方法性能比较

文中统一采用ConvNet作为所有方法的训练网络，与DC相比较的核心集选择法有Random，Herding，K-Center和Forgetting，以往的数据蒸馏方法则是DD（Dataset Distillation）。

泛化性分析

这部分实验分析的是某一网络训练出来的合成数据$\mathcal{S}$用于训练其他网络能否达到较好的性能。作者对6种网络进行了一一组合。

缩合数据数量

这部分分析的是每个类别生成几张缩合图片合适，作者分析了1，10和50三种情况，结果当然是越多效果越好。

应用场景

作者对数据缩合可能存在的两大应用场景进行了分析。

持续学习

持续学习（Continual Learning）是一种将旧任务学习的知识应用到新的任务上、同时在旧任务上的表现不会出现太大的损失的机器学习方法。本质上是基于旧有的模型训练面向新任务的模型，使得最终的模型在新旧任务上都能表现得很好。相比于普通的数据，数据缩合后的合成数据有效信息更多，很适合持续学习。

神经网络架构检索

选择合适的神经网络架构需要训练大量的模型，而数据量更小的合成数据显然能大大地降低训练的算力和存储开销。