Paper003: Dataset Distillation by Matching Training Trajectories

Posted on Edited on In Views: Word count in article: 600 Reading time ≈ 2 mins.
这篇论文发表于前两篇论文之后，但它没有受到Distribution Matching的影响，试着融合核心集法和蒸馏法，而是回到了最原始的参数匹配法。它对原始的参数匹配法进行了改进，并取得了较好的性能，且内存消耗和速度也有了较大的优化。

专家轨迹

专家轨迹（Expert trajectories）$\tau^*$是本文对原训练集训练模型时模型参数变化过程的描述。它记录了每个时期（Epoch）所有模型参数$\theta^*$的值$\left\{\theta_t^*\right\}_0^T$，其中$T$是总的时期数。专家轨迹是在原训练集上得到的，因此其反映了用合成集训练模型时的理论最佳路线。与专家轨迹各时期值相对应地，合成集在时期$t$的模型参数称学生参数（Student parameters）$\hat{\theta}_t$。

短期和长期参数匹配

本文的核心思想是用经过了$N$步优化的$\hat{\theta} _{t+N}$去匹配同一个网络下某一个专家轨迹的$\theta ^* _{t+M}$，其中学生参数$\hat{\theta}_t$被初始化为某个时期的专家参数$\theta_t^*$且$N<<M$。$\hat{\theta} _{t+N}$和$\theta ^* _{t+M}$之间的差异被定义为损失函数$\mathcal{L}$：

$$
\mathcal{L}=\frac{||\hat{\theta} _{t+N}-\theta ^* _{t+M}||_2^2}{||\theta ^* _t-\theta ^* _{t+M}||_2^2}\tag{1}
$$

式中，下标2表示$L_2$范数，即欧几里得范数，定义为向量各元素平方和的平方根；上标2表示平方。之所以要有分母是为了保证当选取的$t$为训练的较后时期、模型参数变化不大时，$L$仍能有较大的响应。以该损失函数$L$进行梯度下降，更新合成集$\mathcal{D} _{syn}$，使得经过多次迭代后，合成集$\mathcal{D} {syn}$训练得到的$\hat{\theta}{t+N}$能使$\mathcal{L}$最小。

1

Fig. 1. Expert trajectories matching (Iteration here means epoch)

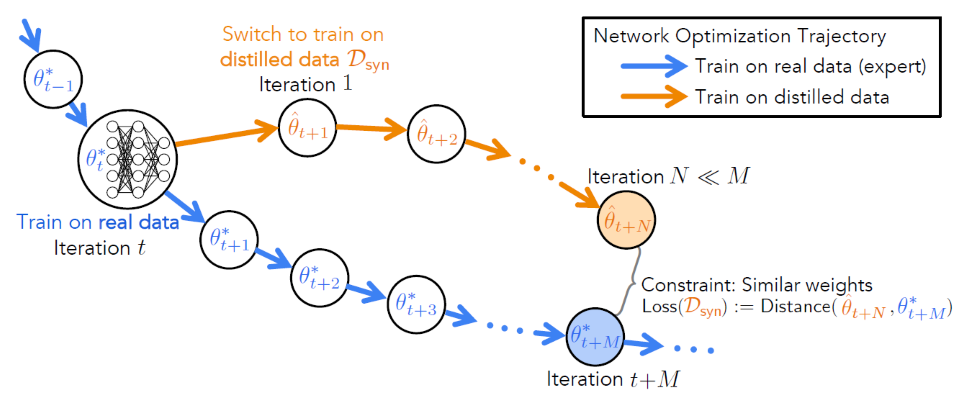
从$N$和$M$的视角来看，之前的数据蒸馏方法，包括最原始的数据蒸馏——只匹配最终的模型参数和基于梯度匹配的数据缩合——实际上是对每个时期的模型参数都进行匹配，都可以被视为$N$和$M$在不同取值下的特例：

2

Fig. 2. Left: Original dataset distillation. Mid: Gradient matching. Right: Expert trajectories

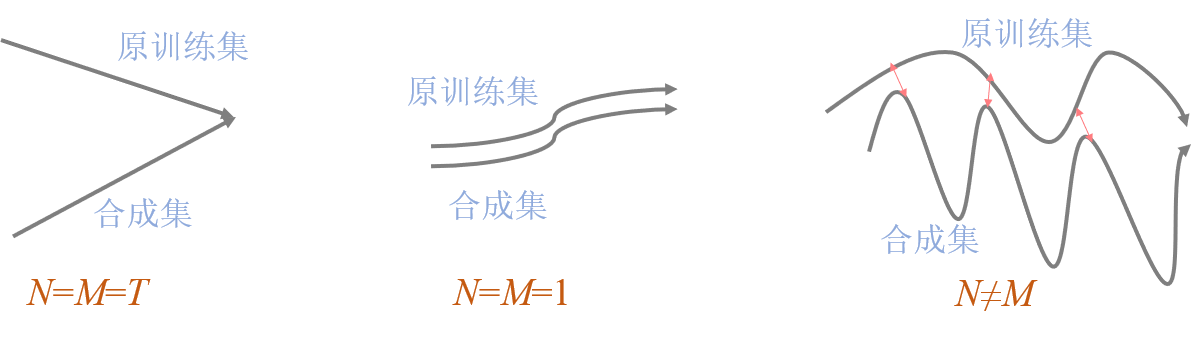
原始的数据蒸馏只考虑结果，因此性能不是太好；梯度匹配过于追求过程，是一种贪心的思想，可能不能得到全局最优且计算量偏大；本文提出的专家轨迹则可视为对前两者的折中。