Graph Neural Networks & Graph Convolutional Networks

数据的图表示

要完整地表示一张图，需要四类信息：顶点（nodes，V），边（edgs，E），全局信息（global-context，U）和连接性（connectivity，A）。其中，每个顶点（Fig 1中黄色的圈）的属性都可以用一个标量或向量表示；每条边（Fig 1中蓝色的线）的属性也可以用一个标量或向量表示；全局信息（Fig 1中红色虚线框）同样可以用一个标量或向量表示。表示图连接性的方法最简单的是邻接矩阵（Adjacency matrix），因为它很容易向量化，但是，邻接矩阵存在两个缺点：1）浪费空间，特别是对于稀疏图；2）对相同的图可以有多种邻接矩阵表示（如调整行列的顶点顺序可以得到不同的邻接矩阵）。这两个缺点，特别是第二个，使得邻接矩阵法不能得到很好的效果。更为有效、常用的方法是邻接列表法，即将每条边用顶点的二元元组表示，所有的边组成一个列表。对于Fig 1中的图，假设顶点顺时针排序，最上面的顶点编号为1，则其连接性可表示为：

$$
[[1, 2], [1, 3], [1, 4], [1, 5], [2, 5], [3, 4]]
$$

Fig. 1. Graph

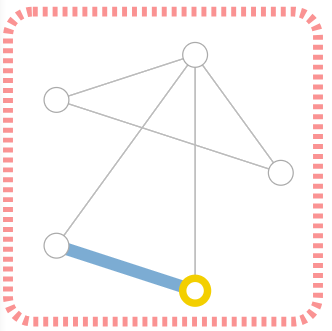
图片的图表示

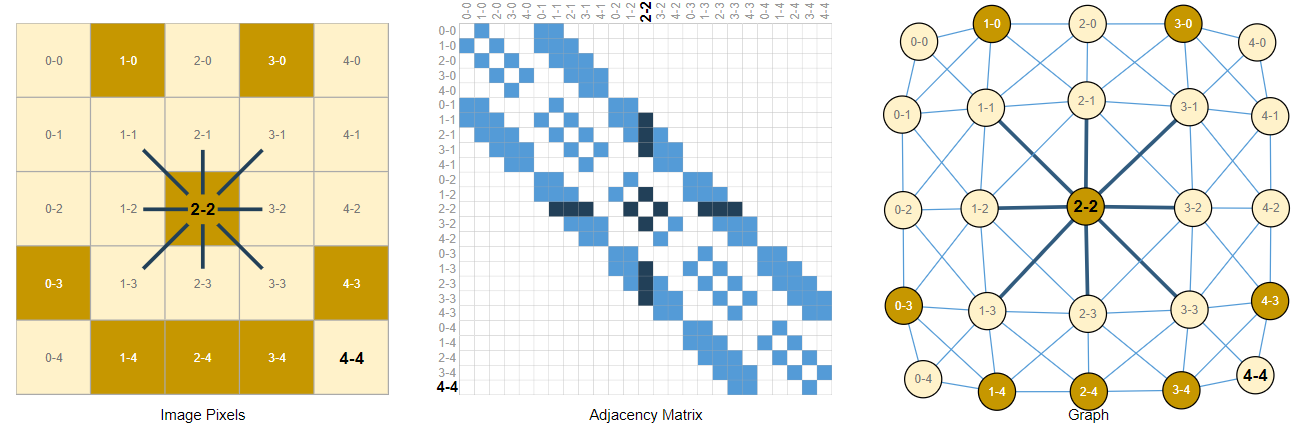
图片是由多个像素点组成的矩阵，因此它可以很自然地被视为一个矩形的特殊的图：每个像素点为顶点，每个像素点和它周围的所有像素点（包括对角线的）具有连接性，像素点的值代表的顶点的属性。

Fig. 2. Image graph

文本的图表示

文本作为一种序列，实际上是一种特殊的图：直线。因此，文本的图表示是一个有向图。

Fig. 3. Text graph

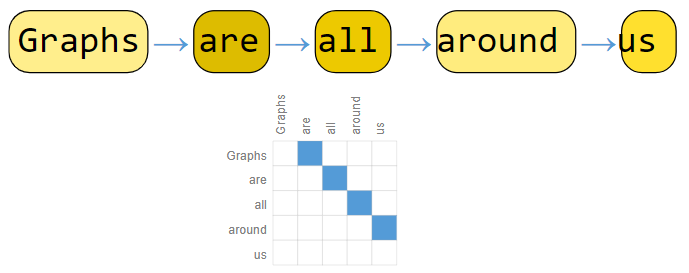
实际上图片和文本连接性的表示要更加简洁，因为所有图片和文本都具有相同的连接模式：图片中的像素只和周围的像素相连；文本中的词元只指向下一个词元，邻接矩阵是条对角线。

由于树也是一种特殊的图，凡是能表示为树的东西，也能用GNNs的方法处理。

面向GNNs的任务

GNNs能解决的任务一般可分三个类别：图级别任务（Graph-level task），顶点级别任务（Node-level task）和边级别任务（Edge-level task）。

对于图级别的任务，最常规的是图分类问题，它和MNIST和CIFAR等图片分类一样，将不同类型的图分到合适的类别。

Fig. 4. Graph-level task

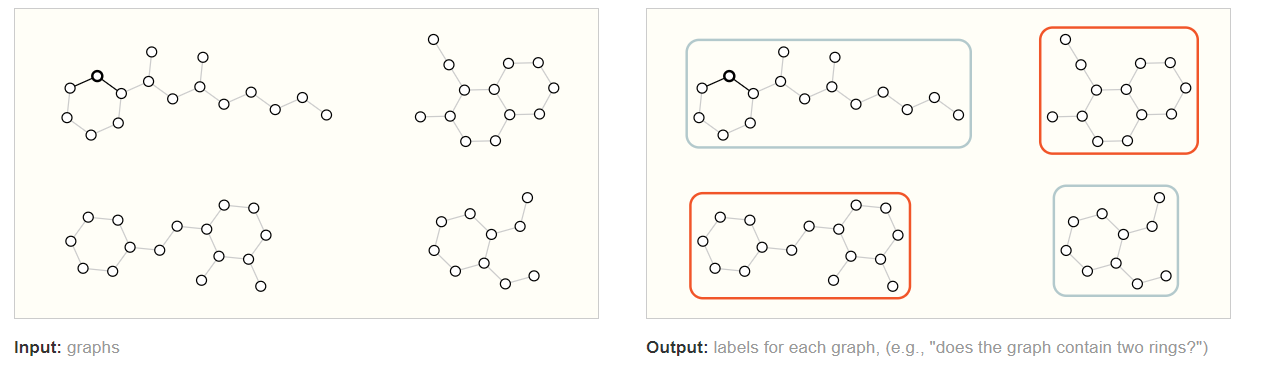
对于顶点级别的任务，最常规的亦为分类问题，即预测顶点的属性或者类别。

Fig. 5. Node-level task

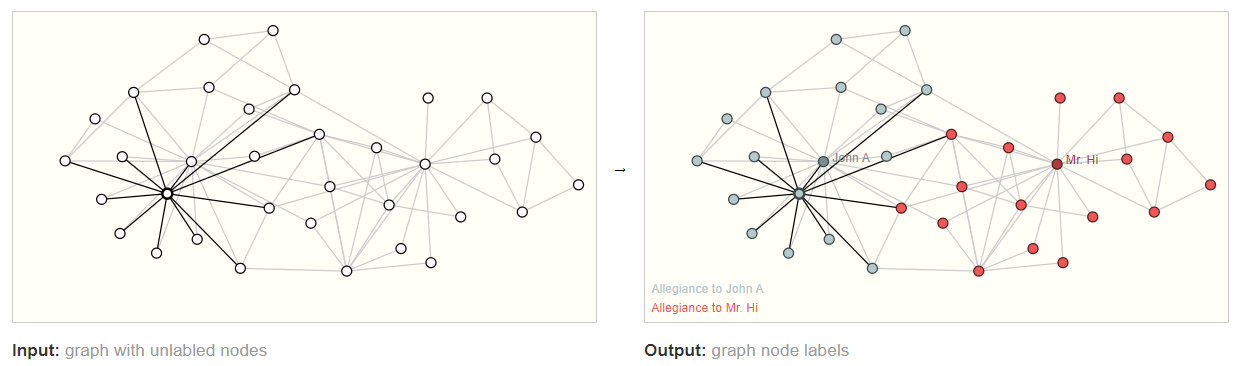
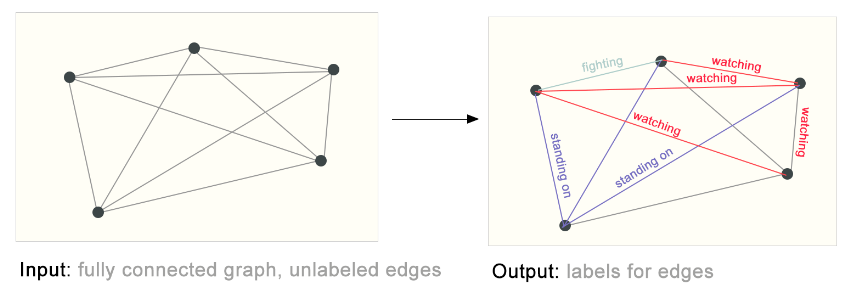
对于边级别的任务，其可以处理的是广义上的分类问题，即预测边的属性（其属性体现着边连接的两个顶点的关系）。

Fig. 6. Edge-level task

图神经网络（GNNs）

图神经网络是一种对图的属性做变换（顶点，边以及全局信息），但是不改变图的拓扑结构的神经网络。它接受图输入，并输出一个属性变化了但拓扑结构不变的图。

Fig. 7. The simplest GNN

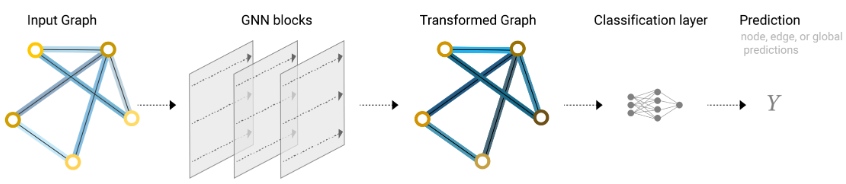
最简单的图神经网络如上图所示。所有的顶点的属性、边的属性和全局信息分别形成一个矩阵，它们分别被输入到一个MLP中。三个MLP形成一个GNN块，每个GNN块的输出都是属性变化后的顶点、边和全局信息，但是图的拓扑结构不变。GNN块可以逐个堆叠，起着特征提取的作用。GNN块实际上相当于一个特征提取器/编码器，而具体的任务则由后续的分类器/解码器完成。

Fig. 8. GNN block

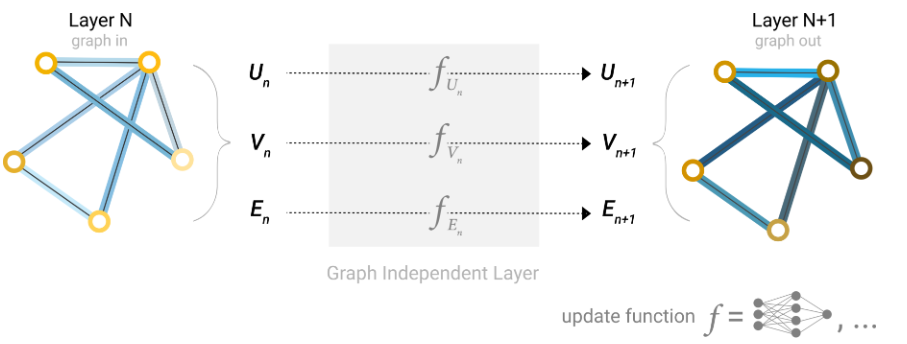
需要注意的是，编码器提取的是顶点、边和全局信息的特征，而输入解码器的特征只是需要的特征，如顶点级别任务只输入顶点特征、边级别任务只输入边特征。不过有些时候给定的图可能缺乏某个方面的信息，它可能只有边属性和全局信息而没有顶点属性，也可能只有顶点属性和边属性而没有全局属性。这时，编码器的工作照常进行，而解码器在工作之前，需要从其他地方获取缺失的信息，该操作称为Pooling。

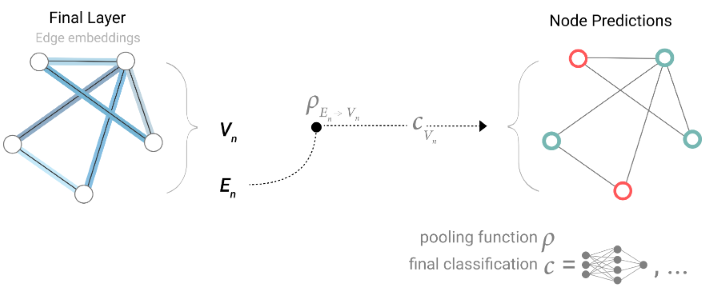
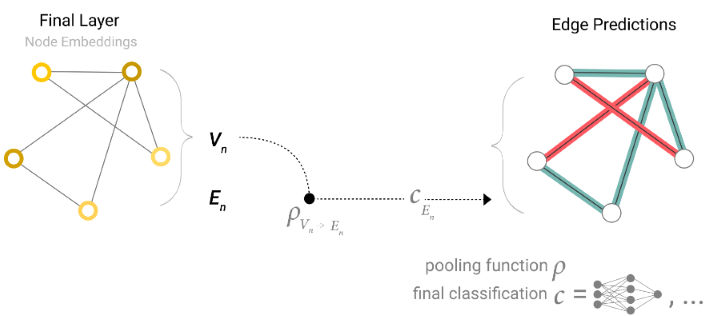
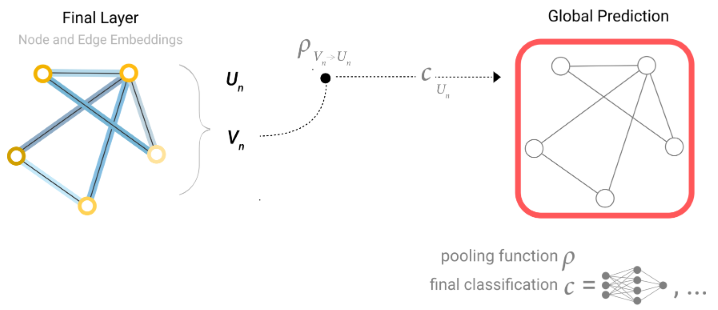
比如，若缺失顶点信息，那么，进入解码器的顶点信息则由包含该顶点的边和全局信息Pooling而来，如Fig 9所示；若缺失边信息，那么，进入编码器的边信息则由该边两侧的顶点和全局信息Pooling而来，如Fig 10所示；若缺失全局信息，那么，进入编码器的全局信息则由所有的顶点信息（也可以加上边的信息）Pooling而来，如Fig 11所示。

顶点、边和全局信息的形状可能不一样，这时候就需要先进行投影。汇聚（Pooling）的方法有多种，如取最大（Max）、求和（Sum）、求和取平均（Average），各种方法的效果差不多。

全局信息相当于一个特殊顶点的属性：这个顶点和所有顶点相连、和所有边相连。因此，全局信息的汇聚会用到所有的顶点和边。

Fig. 9. Node pooling

Fig. 10. Edge pooling

Fig. 11. Graph-context pooling

上述的简单的GNN存在一个严重的缺陷：除了汇聚层，我们没有用到任何连接性的信息。每个顶点、边、全局信息都是被独立地处理的，而它们实际上存在很强的关系。

图卷积神经网络（GCNs）

图卷积神经网络能够解决前面提到的简单图神经网络的缺点。它采用类似于图片卷积的方法，用图卷积层将某一顶点和其周围顶点的信息汇聚到下一层的同一个顶点中，如此，只要经过足够多的图卷积层，单一的顶点就能看到所有顶点的信息。

Fig. 12. GCN layer

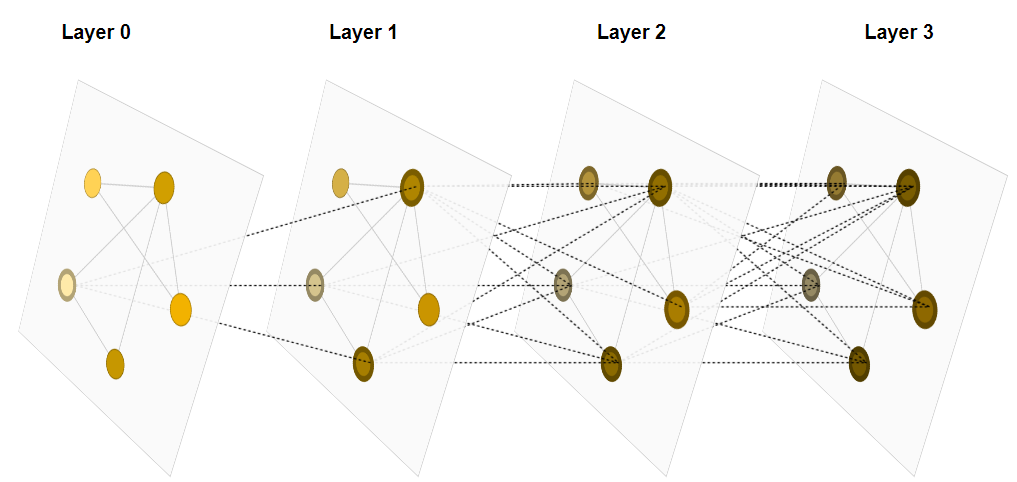
更进一步地，可以将上一节中顶点、边和全局信息间的信息传递提前到图卷积层中。也就是说，边的信息会汇聚边和两边顶点的信息，顶点的信息会汇聚边以及相连顶点的信息。不同的汇聚策略会产生不同的图卷积方法，如下图所示。

Fig. 13. Different ways to combine nodes and edges

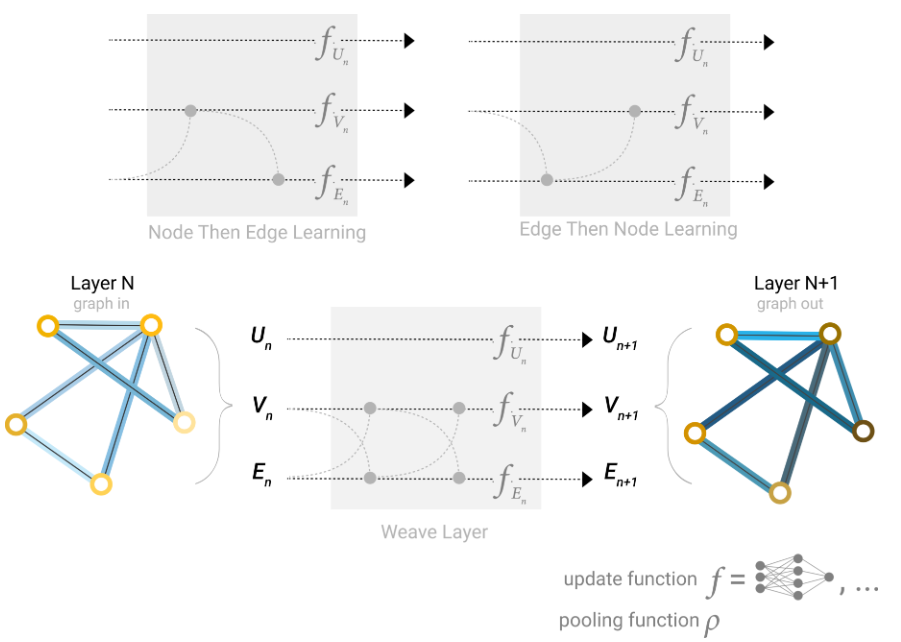
由于顶点和边的属性向量的形状可能不同，汇聚时可以采用映射后再相加或者直接拼接等方法，不同的方法会产生不同的效果。

当我们想要尽早地了解到整个图的情况时，也可以将全局信息加入汇聚操作中。

Fig. 14. Pooling with global-context

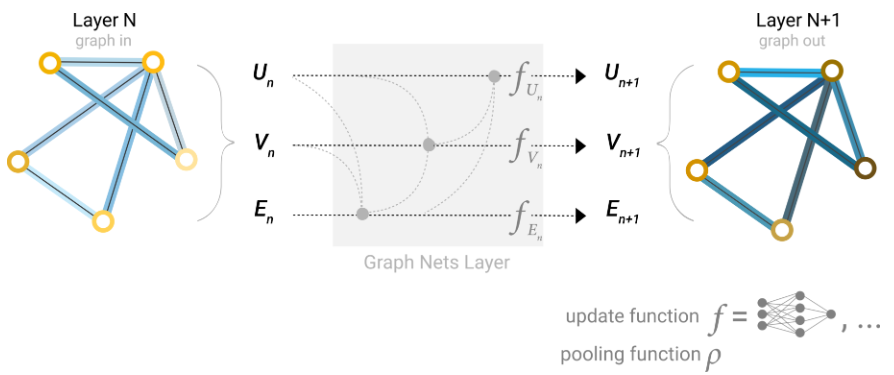
最后一个图卷积层的顶点往往会包含很多信息，这使得我们不得不保留一个很大的计算图以计算梯度，这十分浪费内存和时间。常用的策略是对图进行随机采样，用随机生成的子图来完成训练。采样方法有多种，如Diffusion sampling，Random node sampling，Random walk sampling等。

参考

本文所有的内容包括图片都基于文章 A Gentle Introduction to Graph Neural Networks 以及李沐先生的讲解。

• A Gentle Introduction to Graph Neural Networks
• 零基础多图详解图神经网络（GNN/GCN）【论文精读】