Laplacian
定义
拉普拉斯算子$\Delta$定义为函数$f$(假设$f$为三元函数)的梯度的散度,它接受标量函数输入,并输入一个新的标量函数,即:
$$
\Delta f=\text{div}(\text{grad}f(x,y,z))
$$
哈密顿算子
哈密顿算子$\nabla$定义为:
$$
\nabla=\frac{\partial}{\partial x}\vec{i}+\frac{\partial}{\partial y}\vec{j}+\frac{\partial}{\partial z}\vec{k}
$$
它本身没有意义,只是一个算子,但是又被看作是一个矢量。哈密顿算子作用于标量$f$可以得到$f$的梯度,作用于矢量$\vec{f}$可以得到$\vec{f}$的散度。
梯度
梯度是一个矢量,它表示某一空间函数$f(x,y,z)$在点$(x,y,z)$处方向导数最大的方向或者说函数值变化最快的方向:
$$
\text{grad}f(x,y,z)=\nabla f(x,y,z)=\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}+\frac{\partial f}{\partial z}\vec{k}
$$
散度
散度是一个标量,它表示空间中的矢量场$F=<f,g,h>$在该点$(x,y,z)$单位体积上的通量,即该矢量场发散的强弱程度:
$$
\text{div}(F)=\nabla\cdot<f,g,h>=\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}+\frac{\partial h}{\partial z}
$$
当散度大于0时,表示该矢量场有散发通量的正源;当散度小于0时,表示该矢量场有吸收通量的负源;当散度等于0时,表示该场无源。
拉普拉斯算子的意义
以下以二元函数$f(x,y)$为例,说明拉普拉斯算子的数学意义。
对于给定的二元函数$f(x,y)$,其梯度$\nabla f$给出了其在二维空间上各个点函数值变化最快的方向。
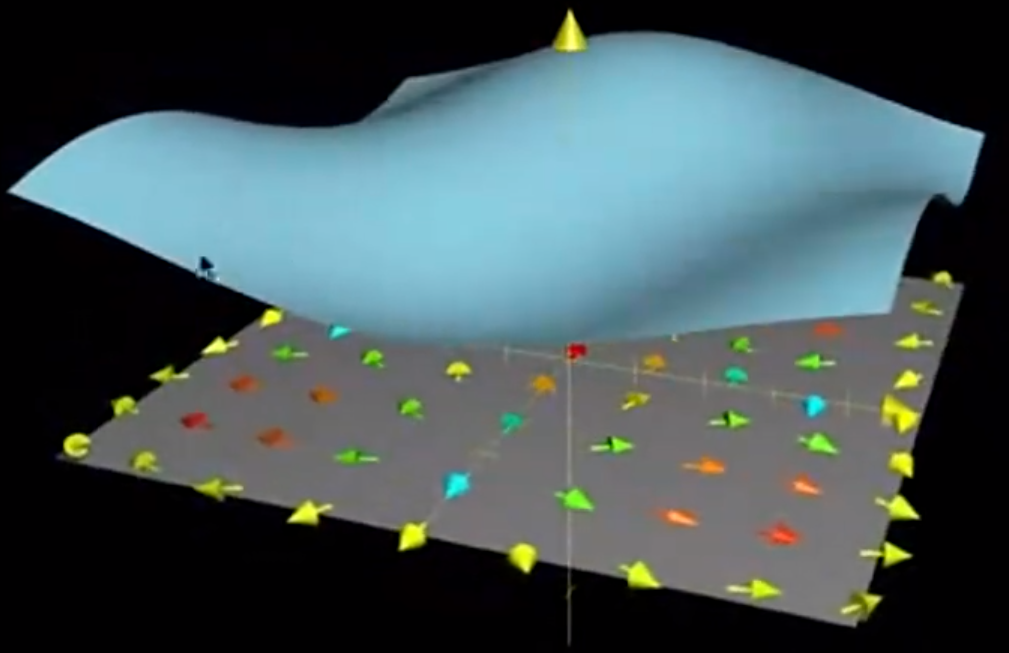
上图下方的箭头即为$f$在各个点上的梯度方向。此时,若我们将原函数图像去掉,我们就得到一个由原函数的梯度向量形成的矢量场:

对该矢量场求散度$\nabla\cdot\nabla f$,我们实际上就能够得到原函数图像的凹凸性(大于0为凸,小于0为凹),如同一元函数的凹凸性一般,多元函数的凹凸性也体现了该点的函数值与该点周围的点的函数值的大小关系,凸说明该点的函数值小于周围点函数值的平均值,凹则说明大于。
这就是拉普拉斯算子($\Delta=\nabla\cdot\nabla=\nabla ^2$),它代表了小范围的凹凸性,这也是它能被用于图像边缘检测的原因(边缘往往显著区别于邻居)。
拉普拉斯矩阵
拉普拉斯矩阵$L$,是图上的拉普拉斯算子,也即离散的拉普拉斯算子。前面提到的拉普拉斯算子,其基于的空间都是连续的,而对于图像的像素矩阵,它可以被视为一个二元的函数,只不过其空间位置(即矩阵的行和列)是离散的值。当拉普拉斯算子作用于离散的空间,拉普拉斯算子就成了拉普拉斯矩阵。
一维和二维离散函数的导数
假设离散空间中空间位置的最小步长为$h$:
$$
x _{i+1}- x_i=...=x_2-x_1=h
$$
将$f(x _{i+1})$和$f(x _{i-1})$分别用泰勒级数在$x_i$点展开:
$$
\begin{align*}
f(x _{i+1})&=f(x_i)+f'(x_i)h+f''(x_i)\frac{h^2}{2}+...\tag{1}\\
f(x _{i-1})&=f(x_i)-f'(x_i)h+f''(x_i)\frac{h^2}{2}-... \tag{2}
\end{align*}
$$
$(1)$和$(2)$相减,可得:
$$
f'(x_i)=\frac{f(x _{i+1})-f(x _{i-1})}{2h}-O(h^2)
$$
同样地,$(1)$和$(2)$相加,可得:
$$
f''(x_i)=\frac{f(x _{i+1})+f(x _{i-1})-2f(x_i)}{h^2}-O(h^3)
$$
若忽略掉低阶无穷小$O(h^2)$和$O(h^3)$,并取$h$为1,那么二维空间的离散拉普拉斯算子便可表示为:
$$
\begin{align*}
\Delta f&=f _{xx}+f _{yy}\\
&=f(x+1,y)+f(x-1,y)-2f(x,y)+f(x,y+1)+f(x,y-1)-2f(x,y)\\
&=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)\tag{3}
\end{align*}
$$
若将3x3的卷积核的中心定义为$(x,y)$:
$$
\begin{bmatrix}
(x-1,y-1)&(x,y-1)&(x+1,y-1)\\
(x-1,y)&(x,y)&(x+1,y)\\
(x-1,y+1)&(x,y+1)&(x+1,y+1)
\end{bmatrix}
$$
则其系数即为用于边缘检测的卷积核:
$$
\begin{bmatrix}
0&1&0\\
1&-4&1\\
0&1&0
\end{bmatrix}
$$
此处可以看出拉普拉斯算子的另外一层含义:$f(x,y)$受到微小扰动后,可能变成$f(x-1,y)$,$f(x,y-1)$,$f(x+1,y)$和$f(x,y+1)$中的任何一个。拉普拉斯算子计算的就是对该点进行微小扰动后可能获得的总增益。这对于连续的拉普拉斯算子也成立,只不过扰动后可能出现的情况变成无数个。增益越大,说明函数在该点越有可能是个凸点(谷点)。
图拉普拉斯矩阵
对于有$N$个顶点的图,其每个顶点的最大邻接顶点数(自由度)为$N$,邻接矩阵为$A$,度矩阵为$D$,其中:
$$
D=
\begin{cases}
D _{ii}=\sum\limits _{j=1} ^{N}A _{ij}\\
D _{ij}=0,i\ne j
\end{cases}
$$
根据扰动与增益的定义,我们很容易将式$(3)$推广到图中。图的扰动增益可以定义为邻接的两个顶点的特征差值。假设顶点$v _i$的特征为$f_i$,那么整个图的顶点特征则为:
$$
f=[f_1,f_2,...,f_N]^T
$$
两邻接顶点的差异可定义为:
$$
f_i-f_j
$$
若考虑加权图中边的权值,则为:
$$
w _{ij}(f_i-f_j)
$$
于是,对某一个顶点$v_i$,其拉普拉斯算子为:
$$
\begin{align*}
\Delta f_i
&=\sum\limits _{j=1} ^Nw _{ij}(f_i-f_j)\\
&=\sum\limits _{j=1} ^Nw _{ij}f_i-\sum\limits _{j=1} ^Nw _{ij}f_j\\
&=D _{ii}f _i-w _{i:}f
\end{align*}
$$
式中,$D _{ii}$为顶点$v_i$的度(有权则为带权的度),$w _{i:}$为顶点$v_i$的邻接边的权重向量,维度为$N$。对于整张图,则为:
$$
\begin{align*}
\Delta f
&=
\begin{pmatrix}
\Delta f_1\\
\Delta f_2\\
...\\
\Delta f_N
\end{pmatrix}=
\begin{pmatrix}
D _{11}f _1-w _{1:}f\\
D _{22}f _2-w _{2:}f\\
...\\
D _{NN}f _N-w _{N:}f
\end{pmatrix}\\
&=
\begin{pmatrix}
D _{11}&\cdots&0\\
\vdots&\ddots&0\\
0&\cdots&D _{NN}
\end{pmatrix}f-
\begin{pmatrix}
W _{11}&\cdots&W _{1N}\\
\vdots&\ddots&\vdots\\
W _{N1}&\cdots&W _{NN}
\end{pmatrix}f\\
&=(D-W)f\\
&=Lf
\end{align*}
$$
$L$称拉普拉斯矩阵。若$W$不表示权重,只表示邻接关系,则$W$即为邻接矩阵$A$。
拉普拉斯矩阵是半正定矩阵,即对于任意不为0的实列向量$x$,有$x^TLx\ge0$。
此处不以符号区别行/列向量,均假设其自适应。
邻接矩阵探讨
邻接矩阵$A$实际上也相当于一个算子,如:
$$
\begin{align*}
g&=Af\\
g(i)&=\sum _{j} ^{A _{ij}=1}f _j
\end{align*}
$$
$g(i)$表示$i$的邻接顶点的特征和。又如:
$$
\begin{align*}
f ^Tg
&=f ^TAf\\
&=\sum\limits _{i,j} ^{A _{ij}=1}f _i\cdot f _j
\end{align*}
$$
邻接矩阵必是对称矩阵,因此这实际上是个二次形。
拉普拉斯矩阵探讨
类似地,拉普拉斯矩阵$L$和$f$也能形成二次型:
$$
\begin{align*}
f^TLf
&=\sum _{(i,j)\in E}(f _i - f _j)^2\tag{4}
\end{align*}
$$
该式具有实际的物理意义:

在上图所示弹簧网络中,有5个质子,假设两端(黑球)固定,并给予中间的三个振子一定程度的扰动,则当系统重新平衡时,三个振子和两端会停留在让系统总弹性势能最小的位置。假设连接质子$i$和质子$j$的弹簧的弹性系数为$k _{ij}$($k _{ji}$),则系统的总弹性势能为:
$$
E=\frac{1}{2}\sum _{(i,j)\in E}k _{ij}(x(i)-x(j))^2\tag{5}
$$
式中,$i$和$j$表示质子,$x(i)$为质子$i$的绝对位置,$E$是边集(即弹簧集)。最终质子的位置将使得$E$最小。将上述弹簧网络扩展为更一般的图,那么式$(5)$便能很轻易地被扩展为式$(4)$,只不过省略了一些对结果不造成影响的项(e.g. $\frac{1}{2}$),且一些项的含义发生了变化(e.g. $k _{ij}$成了图的边的权,若图的边无权,则可忽略该项)。式$(4)$显然是一个凸函数,因此它可以作为图神经网络的损失函数(但一般作为正则项)。
关联矩阵
关联矩阵$\nabla$展现了边和其两端顶点的关系。一般地,有向图的关联矩阵更有意义,因此,对于无向图,我们可以为每条边随意规定一个方向,并定义其关联矩阵(形状为$|E|\times|V|$)为:
$$
\nabla=
\begin{cases}
\nabla _{ev}=-1,&\text{if v is the initial vextex of e}\\
\nabla _{ev}=1,&\text{if v is the terminal vextex of e}\\
\nabla _{ev}=0,&\text{otherwise}
\end{cases}
$$
关联矩阵与拉普拉斯矩阵存在关系:
$$
L=\nabla^T\nabla
$$
拉普拉斯谱分解
特征分解也叫谱分解,即将矩阵分解为特征值和特征向量的乘积。因为拉普拉斯矩阵$L$为对称矩阵,因此它有$N$个特征值,$N$个相互正交的特征向量:
$$
\begin{align*}
Lu_k&=\lambda_ku_k\\
L=U^{-1}\Lambda&U=U^T\Lambda U
\end{align*}
$$
拉普拉斯矩阵的正则化
首先,要了解邻接矩阵的正则化:
$$
\tilde{A}=D ^{-\frac{1}{2}}A D ^{-\frac{1}{2}}
$$
如同一般的正则化一样,邻接矩阵的正则化也可视作一种防止过拟合的措施。但是,邻接矩阵的正则化包含了两个方向的正则:
- 左乘$D ^{-\frac{1}{2}}$是横向正则,即对$A$的同一行用相同尺度放缩,而对$A$的不同行用不同尺度放缩,这在一定程度上使得度高的顶点和度低的顶点在聚合后值不会相差得太太,有点像BatchNorm;
- 右乘$D ^{-\frac{1}{2}}$是纵向正则,即对$A$的同一列用相同尺度放缩,而对$A$的不同列用不同尺度放缩,这相当于为邻接顶点赋予分发比例,即,对某个邻接顶点$j$,其信号聚合到本顶点$i$时,其贡献的程度应该是$1/D _{jj}$,当然,实际上是$1/\sqrt{D _{jj}}$,这是为了保证左右正则后的行列式值与只用$D$左正则的值相同。
同样地,拉普拉斯矩阵的正则化为:
$$
\begin{align*}
\tilde{L}
&=D ^{-\frac{1}{2}}L D ^{-\frac{1}{2}}\\
&=D ^{-\frac{1}{2}}(D-A) D ^{-\frac{1}{2}}\\
&=I-D ^{-\frac{1}{2}}A D ^{-\frac{1}{2}}
\end{align*}
$$
上式本质上是让对角线都变成1。
注,此处假设图不带权,故用的是邻接矩阵$A$。
正则化拉普拉斯矩阵仍为半正定对称矩阵,且所有特征值$\lambda\in[0,2]$