Graph Fourier Transform
傅里叶变换
在探讨图傅里叶变换之前,我们需要先弄清楚傅里叶变换和傅里叶逆变换的本质。傅里叶逆变换本质上是傅里叶级数在非周期函数(周期为$\infty$)上的形式,因此,傅里叶逆变换将一个函数表示为若干正交基函数的线性组合。与之相应地,傅里叶变换就是求线性组合的系数
$$
\begin{align*}
f(t)=\frac{1}{2\pi}\int_{-\infty} ^{+\infty}&\int_{-\infty} ^{+\infty}f(t)e^{-i\omega t}dt\space e^{i\omega t}d\omega\tag{1}\\
F(\omega)=&\int_{-\infty} ^{+\infty}f(t)e^{-i\omega t}dt\tag{2}
\end{align*}
$$
其中,式$(1)$为傅里叶逆变换,式$(2)$为傅里叶变换。
见Fourier Transform了解傅里叶变换的推导过程。
图傅里叶变换
图的顶点$i$可表示为信号$f_i$,其中$f _i\in\mathbf{R} ^F$,假设图有$N$个顶点,则整张图可以表示为:
$$
f=[f_1,f_2,...,f_N]^T
$$
图傅里叶逆变换,使用的是拉普拉斯矩阵$L$的特征向量作为基函数(Fourier bias)。因为拉普拉斯矩阵是个半正定对称矩阵,所以它有$N$个相互正交的特征向量$\vec{u} _i$(见Laplacian了解拉普拉斯变换和拉普拉斯矩阵)。若使用拉普拉斯矩阵的特征向量作为图傅里叶逆变换的基函数,则图上的任意信号就可以表示为:
$$
\begin{align*}
f&=\hat{f}(\lambda _1)\vec{u} _1+...+\hat{f}(\lambda _N)\vec{u} _N\\
&=U\hat{f}
\end{align*}
$$
式中,$U$为使拉普拉斯矩阵$L$的相似对角化的正交矩阵,$\hat{f}$为$f$的傅里叶系数,也是其在频域的信号。这本质上是一次坐标变换,即,将$f$在时域的坐标,转变为以$(\vec{u _1},...,\vec{u} _n)$为正交基的频域坐标$\hat{f}$。见Fourier Transform And CNN 了解傅里叶变换和坐标变换的关系。由于$U$是正交矩阵,我们可以很容易得到$f$的傅里叶变换为:
$$
\hat{f}=U ^Tf
$$
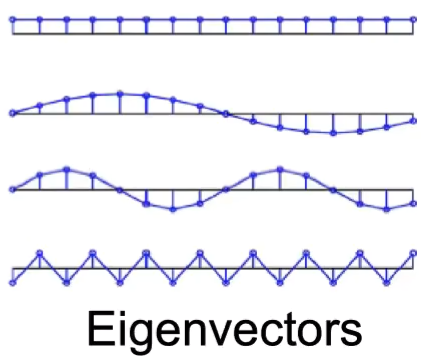
实际上,正交的特征向量$\vec{u _i}$就是离散形式的正(余)弦波形: