Spectral Approaches
从卷积到傅里叶变换
图的顶点$i$可表示为信号$f_i$,其中$f _i\in\mathbf{R} ^F$,假设图有$N$个顶点,则整张图可以表示为:
$$
f=[f_1,f_2,...,f_N]^T
$$
基于卷积的理论及其与傅里叶变换的关系(卷积的傅里叶变换等于傅里叶变换的乘积),卷积操作可以定义为:
$$
\begin{align*}
g\star f
&=\mathcal{F} ^{-1}[\mathcal{F}(g\star f)]\\
&=\mathcal{F} ^{-1}(\mathcal{F}(g)\odot\mathcal{F}(f))\\
&=U(U ^{T}g\odot U ^{T}f) \tag{1}
\end{align*}
$$
式中,$g$是卷积核,用于提取、汇聚图的空间信息;$U$是图的拉普拉斯矩阵的特征向量矩阵,它被用作离散形式的傅里叶变换的傅里叶基。具体细节见Graph Fourier Transform。式子中$U ^{T}g$称为滤波器(filter)。由于$U ^Tg$实际上是对$g$的傅里叶变换,因此:
$$
U ^{T}g=\hat{g}=[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)]^T
$$
即,它是由$g$所包含的各个特征值$\lambda _i$所对应的正交基$u _i$(相当于连续形式的傅里叶变换的不同频率的正弦波形)在$g$中所占的比重所组成的向量。同样地,$U ^Tf$可转化为:
$$
U ^{T}f=\hat{f}=[\hat{f}(\lambda _1),...,\hat{f}(\lambda _N)]^T
$$
于是它们的哈达玛积($\odot$)就为:
$$
\begin{align*}
U ^{T}g\odot U ^{T}f
&=\hat{g}\odot\hat{f}\\
&=
\begin{bmatrix}
\hat{g}({\lambda _1})\times\hat{f}({\lambda _1})\\
\vdots\\
\hat{g}({\lambda _N})\times\hat{f}({\lambda _N})
\end{bmatrix}
\end{align*}
$$
而:
$$
\begin{bmatrix}
\hat{g}(\lambda _1) &\\
& \ddots \\
& & \hat{g}(\lambda _N)
\end{bmatrix} \cdot
\begin{bmatrix}
\hat{f}({\lambda _1})\\
\vdots\\
\hat{f}({\lambda _N})
\end{bmatrix} =
\begin{bmatrix}
\hat{g}({\lambda _1})\times\hat{f}({\lambda _1})\\
\vdots\\
\hat{g}({\lambda _N})\times\hat{f}({\lambda _N})
\end{bmatrix}
$$
因此,式$(1)$可以变为:
$$
\begin{align*}
g\star f
&=U(U ^{T}g\odot U ^{T}f)\\
&=U(\text{diag}[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)]U ^{T}f)\\
&=U\text{diag}[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)] U ^{T}f\tag{2}
\end{align*}
$$
矩阵结合律是成立的
另一种角度,若从右向左看式$(2)$的最后一个等式,上述卷积操作其实就是一次对图信号$f$的滤波:
- $U^T f$将时域的图信号转换为频域的图信号;
- $\text{diag}[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)](U^T f)$对频域的图信号进行滤波,提取特征;
- $U(\text{diag}[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)]U ^{T}f)$将经过滤波的频域图信号转换回时域。
基于谱方法(Spectral approaches)的图神经网络的发展实际上就是一个设计更好的滤波器$\text{diag}[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)]$的过程。
第一代GCN
为了使得滤波器能够被学习,第一代GCN直接将式$(2)$中的滤波器的对角元素替换为了可学习的参数$w$,于是第一代GCN的卷积操作就变为:
$$
Z=\sigma(Ug_wU ^{T}f)\tag{3}
$$
其中激活函数用于赋予非线性性。上述操作的思路很简单:输入$f$经过第一个卷积层后得到$Z$,$Z$再作为下一个卷积层的输入,逐层地学习、提取信息。然而,缺点也显而易见:需要对拉普拉斯矩阵进行特征分解以得到$U$,而当图顶点数很多时,这样的特征分解是十分困难的。
第二代GCN
鉴于$\text{diag}[\hat{g}(\lambda _1),...,\hat{g}(\lambda _N)]$是特征值对角矩阵$\Lambda$的函数,第二代GCN采用k阶多项式来近似的拟合这个函数,即:
$$
g _w(\Lambda)\approx\sum\limits _{k=0} ^Kw _k\Lambda ^k
$$
将其带入式$(3)$,则第二代GCN为:
$$
\begin{align*}
Z
&=\sigma(Ug_w(\Lambda)U ^{T}f)\\
&=\sigma(U\sum\limits _{k=0} ^Kw _k\Lambda ^kU ^{T}f)\\
&=\sigma(\sum\limits _{k=0} ^Kw _kL ^kf)
\end{align*}
$$
$U\Lambda ^k U ^T=L^k$,其中,$L$为拉普拉斯矩阵。
不难看出,第二代GCN不对拉普拉斯矩阵进行特征分解,而是直接用拉普拉斯矩阵对$f$进行变换。同时,可学习的参数个数也有原来的$N$个下降为$K+1$个。与第一代相比,第二代GCN的计算复杂度明显更低。虽然如此,仍然需要计算$L ^k$,时间复杂度为$O(N ^2)$。
事实上,由于:
$$
L=D-A\tag{4}
$$
其中$A$为邻接矩阵,式$(4)$的证明见图拉普拉斯矩阵。因此:
$$
L ^k=C_k ^0D ^k-C_k ^1D ^{k-1}A+...+(-1) ^kC _k ^kA ^k
$$
式中,由于$D$和$A$都是对称矩阵,所以$DA=AD$。邻接矩阵的$k$次幂的各个元素$A ^k[i][j]$表示的是从$i$到$j$路径长度为$k$的路径的条数。$D$为对角矩阵,只会改变与其相乘的矩阵的非零元素的值。因此,$L ^k$中的$k$实际上就是本次卷积感受野的大小,即距离中心顶点$k+1$-hop以内的邻居顶点都会被用来更新中心顶点的特征表示。
接下来的两类GCN的$L$均代表正则化后的拉普拉斯矩阵。
ChebyNet
不同于第二代GCN,2016年被提出的ChebyNet使用切比雪夫多项式来近似拟合滤波器:
$$
\begin{cases}
g _w=\sum\limits _{k=0} ^{K}w _kT _k(\hat{\Lambda})\tag{5}\\
\hat{\Lambda}=\frac{2}{\lambda _{max}}\Lambda-I _N
\end{cases}
$$
其中,$\lambda _{max}$是正则化的拉普拉斯矩阵$L$的最大特征值,而正则化拉普拉斯矩阵的特征值介于0和2之间,因此,$\hat{\Lambda}$的作用是让特征值矩阵的值介于-1和1之间。切比雪夫多项式是递归定义的:
$$
\begin{cases}
T _0(x)=1 \\
T _1(x)=x \\
T _{n+1}(x)=2xT _n(x)- T _{n-1}(x)
\end{cases}
$$
切比雪夫多项式各个幂次项的系数实际上是余弦函数$\cos nx$展开为$\cos x$的函数后的各个幂次的$\cos x$的系数。因此,相比于普通的多项式,切比雪夫多项式具有很多特殊的性质:
- 在$[-1,1]$有$n$个零点;
- 在$[-1,1]$的值在$[-1,1]$之间震荡。
- ...
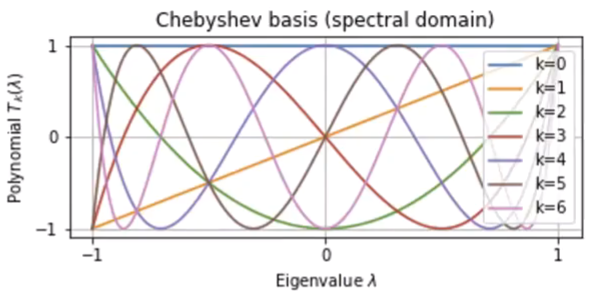
这使得它与正弦波形十分相似,但是又更为简单。将式子带入$(3)$,可得:
$$
\begin{cases}
Z=\sigma(\sum\limits _{k=0} ^Kw _kT _k(\hat{L})f)\\
\hat{L}=\frac{2}{\lambda _{max}}L-I _N
\end{cases}
$$
因为切比雪夫多项式本质上仍是多项式,所以$k$仍然表示的是感受野的大小,这与第二代GCN一致。
GCN
目前常规的GCN源于2017年Kipf等发表的论文。它是在ChebyNet的基础上进一步简化而来的,它取$K$为1,即,只取切比雪夫多项式的前两项:
$$
g _w=w_0+w_1\hat{L}\tag{6}
$$
进一步地,它固定$\lambda _{max}$为2,并且限制$w_0=-w_1=w$,于是式$(6)$变为:
$$
\begin{align*}
g _w
&=w-w(L-I _N)\\
&=-w(L-2I _N)\\
&=-w[D ^{-\frac{1}{2}}(D-A)D ^{-\frac{1}{2}}-2I _N]\\
&=-w(I _N-D ^{-\frac{1}{2}}AD ^{-\frac{1}{2}}-2I _N)\\
&=w(I _N+D ^{-\frac{1}{2}}AD ^{-\frac{1}{2}})\tag{7}
\end{align*}
$$
不难看出,如此,卷积层的感受野就只有1,即中心顶点只会聚合与其直接邻接的顶点的信息。但是,由于$A$的对角线均为0,在卷积过程中,中心顶点会丢失自己的信息。因此,GCN为每个顶点增加了自旋边,即:
$$
\tilde{A}=A+I _N
$$
相应地,拉普拉斯矩阵$L$和和度矩阵$D$分别变成了$\tilde{L}$和$\tilde{D}$。如此,$k$为0的切比雪夫项$I _N$就不再被需要了,因为$\tilde{A}$使得中心顶点能够保留自己的信息,故式$(7)$进一步简化为:
$$
g _w=w\tilde{D} ^{-\frac{1}{2}}\tilde{A}\tilde{D} ^{-\frac{1}{2}}
$$
为了增加可学习的参数,GCN将$w$扩充为矩阵$W$,并定义了卷积层的最终操作为:
$$
Z=\sigma(\tilde{D} ^{-\frac{1}{2}}\tilde{A}\tilde{D} ^{-\frac{1}{2}}fW)
$$
以上就是GCN,它是ChebyNet的简化,但实际效果却远优于更复杂的ChebyNet。但是,GCN不能叠加很多层,因为它是个低通滤波器,即它会过滤掉高频的信号,因此当GCN的层数过高时,最终的信号就只剩低频信号了,相应地网络的效果也会变差:

图中的$h$就是文中的$g$。