Graph Neural Tangent Kernel
Neural Tangent Kernel
对于一个参数$\theta$随机初始化的神经网络$f(x;\theta)$,在小批量随机梯度下降SGD的过程中,训练样本$(x',y')$(此处假设批量大小为1)会使得$f(x;\theta)$向着减小$f(x';\theta)$和$y'$之间误差的方向移动:
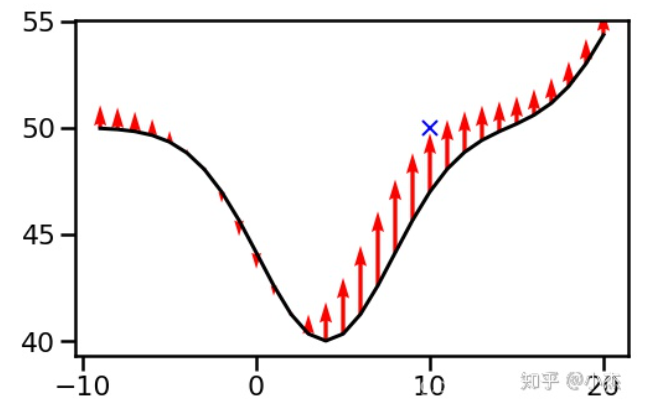
而Neural Tangent Kernel就是一个用于衡量曲线$f(x;\theta)$变化的函数,其定义为:
$$
\eta \mathcal{K}(x,x')=f(x;\theta+\eta \frac{df(x';\theta)}{d\theta})-f(x;\theta)
$$
式中,$\eta$是一个更新步长,即学习率。当学习率无限小时,我们便得到$f(x;\theta)$变化曲线:
$$
\mathcal{K}(x,x')=\text{lim} _{\eta \to0} \frac{f(x;\theta+\eta \frac{df(x';\theta)}{d\theta})-f(x;\theta)}{\eta}
$$
使用一阶泰勒展开,我们可以得到:
$$
\begin{align*}
\mathcal{K}(x,x')
=&\text{lim} _{\eta \to0} \frac{f(x;\theta)+f'(x;\theta)\eta \frac{df(x';\theta)}{d\theta}-f(x;\theta)}{\eta}\\
=&f'(x;\theta)\frac{df(x';\theta)}{d\theta}\\
=&<\frac{df(x;\theta)}{d\theta},\frac{df(x';\theta)}{d\theta}>
\end{align*}
$$
对于Fig. 1,其变化曲线为:
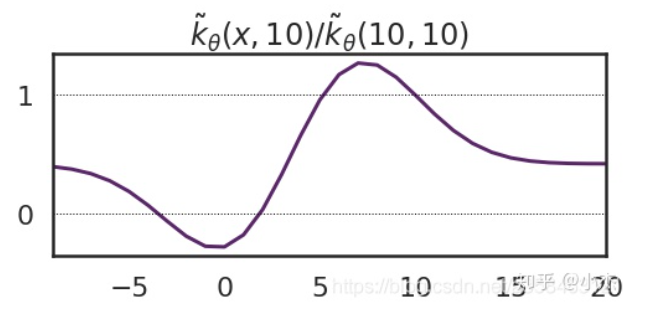
此处假设$(x',y')=(10,50)$。除$\mathcal{K(10,10)}$只是为了标准化。
如果不断地进行SGD,那么最终,$\mathcal{K}(x,x')$和$f(x;\theta)$均会收敛到一个稳定的曲线:
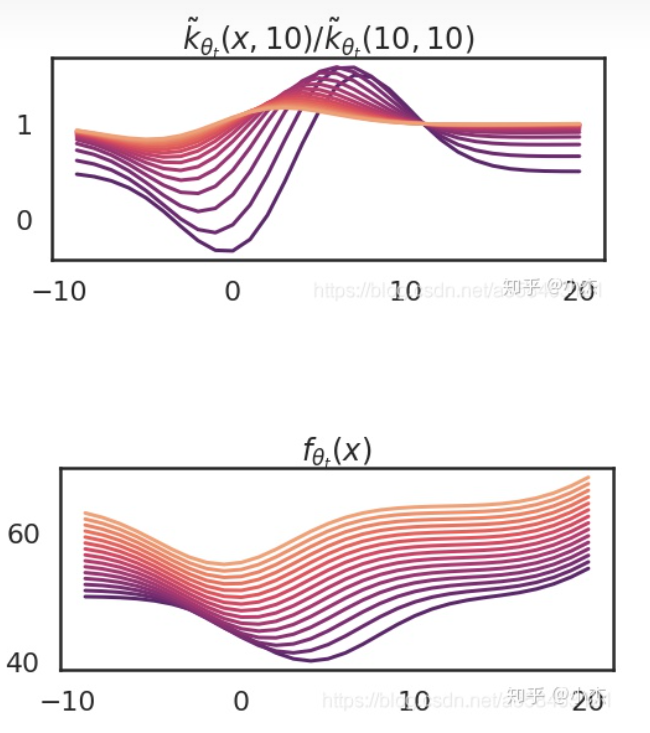
另一方面,若神经网络的宽度足够大,则在SGD的过程中,参数$\theta$的变化将会十分小,$\mathcal{K}$的变化也会非常小,整个神经网络实际上可以用$f(x;\theta)$的一阶泰勒函数拟合:
$$
f(x;\theta)\approx f(x;\theta _0)+\frac{df(x;\theta _0)}{d\theta}(\theta - \theta _0)
$$
上式中,对于确定的初始化$\theta _0$,$f(x;\theta _0)$是常数,而$\frac{df(x;\theta _0)}{d\theta}$是$x$的函数,也就是说,若将$\frac{df(x;\theta _0)}{d\theta}$视作一个整体,则$f(x;\theta)$实际上成为了一个线性函数。而这个将非线性空间的回归转化为线性空间回归的$\frac{df(x;\theta _0)}{d\theta}$就是核方法中的映射函数$\phi(x)$:
$$
\begin{align*}
\phi(x)=&\frac{df(x;\theta _0)}{d\theta}\\
\mathcal{K(x,z)}=\phi(x) ^T\phi(z)=&<\frac{df(x;\theta)}{d\theta},\frac{df(z;\theta)}{d\theta}>
\end{align*}
$$
Neural Tangent Kernel的作用在于,对于无限宽的网络(能拟合任何函数的神经网络),只要参数$\theta$以某种合适的方式初始化,$\mathcal{K}(x,x')$一开始就是收敛值;而对于一般的网络,$\mathcal{K}(x,x')$在训练过程中也会最终收敛,此时,神经网络的训练实际上就是一个Kernel Gradient Descent的过程。即,用SGD训练神经网络等同于拟合核函数。换句话说,此时的神经网络(的隐藏层)本质上是一个映射函数$\phi(x)$。这也解释了为什么复杂的神经网络不仅没有过拟合,反而得到了很强的泛化精度,因为其最终的收敛值无限地接近核方法得到的解析解。
Graph Neural Tangent Kernel
Graph Neural Tangent Kernel是Neural Tangent Kernel在GNN上的应用。它定义:
$$
\mathcal{K}(G,G')=<\frac{df(G;\theta)}{d\theta},\frac{df(G';\theta)}{d\theta}>
$$
其中$G$和$G'$是两张不同的图,$G=(V,E)$,$G'=(V',E')$。最终$\mathcal{K}(G,G')$是个核矩阵,维度为$|V|\times|V'|$。此时,若把$G$当作测试集,而$G'$当作训练集,根据SVM中的预测算法:
$$
\mathcal{K}(G,G')Y'
$$
就是对测试集的预测。
考虑正则则为:
$$
\mathcal{K}(G,G')[\mathcal{K}(G',G')+\lambda I] ^{-1}Y'
$$