Dataset Distillation: A Summary
文中大多数内容都基于Yu et al.的论文Dataset Distillation: A Comprehensive Review。
Performance Matching
Performance Matching,表现/效果匹配,是最先被提出的一种基于机器学习的数据蒸馏方法。这种方法核心思想在于将Synthetic Data视作神经网络中的一个“超参数”,如学习率一般,但不同的是,它是可学习的超参数。其优化过程分两步:
- 用Synthetic Data训练神经网络;
- 将原训练集$\mathcal{T}$输入用Synthetic Data训练的神经网络,计算得到预测的Loss,以该Loss作为损失函数更新Synthetic Data。
最初的基于Performance Matching的方法的精度和训练速度都不怎么样,但后来有学者将第一步中的神经网络替换为了核函数,反而使得Performance Matching超过了多数后来的方法。
Meta Learning Based Methods
该方法最先在Wang et al.的DATASET DISTILLATION中被提出,也是数据蒸馏开山立宗的方法,一般简称DD。Meta Learning也就是把Synthetic Data视作一个可学习的超参数。它获得Synthetic Data的思路就是上面所提到的,基本公式与流程如下:
$$
\begin{align*}
\theta ^{(t)}&=\theta ^{(t-1)}-\eta\nabla l(\mathcal{S};\theta ^{(t-1)})\tag{1}\\
\mathcal{S}^{(\tau)}&=\mathcal{S}^{(\tau-1)}-\eta'\nabla L(\theta^{(T)},\mathcal{T})\tag{2}
\end{align*}
$$
其中,式$(1)$是内层循环,用于更新神经网络,式$(2)$是外层循环,用于更新Synthetic Data。
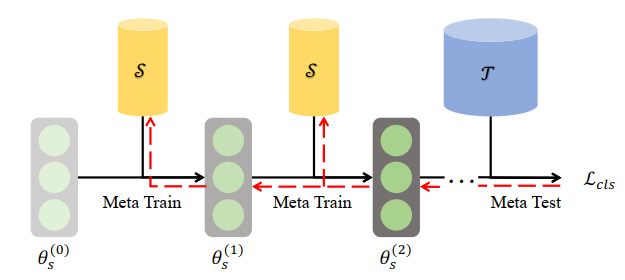
显而易见,这是一种Bi-level Optimization Algorithm:内层循环更新神经网络,外层循环更新Synthetic Data。而内层循环又需要用到Synthetic Data来产生梯度以训练网络,因而Synthetic Data的更新内在地会包含一个二阶导,这是极耗内存和时间的。而实际上蒸馏出来的数据效果也不是特别好。
Kernel Ridge Regression Based Methods
该方法最初在Nguyen et al.的DATASET META-LEARNING FROM KERNEL RIDGEREGRESSION中被提出,一般简称KIP。这种方法是建立在无限宽的全连接层可以用特殊的核函数来拟合这一研究成果的。KIP用到的核函数被称为Neural Tangent Kernel(NTK)。它本质上也是Meta Learning,只不过使用核函数来替代了内层循环,并用Kernel Ridge Regression计算损失函数,使得原本的双层优化变为了一层:
$$
\begin{align*}
L(\mathcal{S},\mathcal{T})&=||Y _\mathcal{T}-K _{X _\mathcal{T}X _\mathcal{S}}(K _{X _\mathcal{S}X _\mathcal{S}}+\lambda I)^{-1}Y _\mathcal{S}||^2\\
\mathcal{S}^{(\tau)}&=\mathcal{S}^{(\tau-1)}-\eta'\nabla L(\mathcal{S},\mathcal{T})
\end{align*}
$$
当然,还有使用其他核函数的版本,但一般用的都是NTK,此处就不再赘述了。
文中还提到了另一个脱胎于Kernel Ridge Regression的方法FRePo,该方法在目前来说取得了最好的蒸馏效果。
Parameter Matching
Parameter Matching,参数匹配,这种方法的想法很直观:要想Synthetic Data取得和训练集相近的泛化精度,只要Synthetic Data训练出来的网路的参数(Parameter)和训练集训练出来的网络的参数相近即可。不过实际上并没有人会直接匹配参数,而是转而去匹配训练过程中的梯度,即让Synthetic Data产生和训练集相近的梯度,因而这类方法也可以叫Gradient Matching。
Single-Step Parameter Matching
Single-Step Parameter Matching在DATASET CONDENSATION WITH GRADIENT MATCHING中被Zhao et al.提出,是最先被提出的基于参数匹配的数据蒸馏方法,一般称DC。其核心思想很简单:
- 训练集$\mathcal{T}$和Synthetic Data $\mathcal{S}$分别过一次神经网络;
- 分别计算梯度;
- 计算梯度差异,作为$Loss$;
- 更新Synthetic Data,用更新后的Synthetic Data更新神经网络。
文中用到的作为$Loss$的梯度差异函数为$\cos$函数,即更关心梯度的方向:
$$
Loss(\mathcal{S},\mathcal{T})=1-\frac{grad(\mathcal{S})\cdot grad(\mathcal{T})}{||grad(\mathcal{S})||\space||grad(\mathcal{T})||}
$$
上面的$grad$是指输入数据在神经网络上所产生的梯度。基本流程如下:
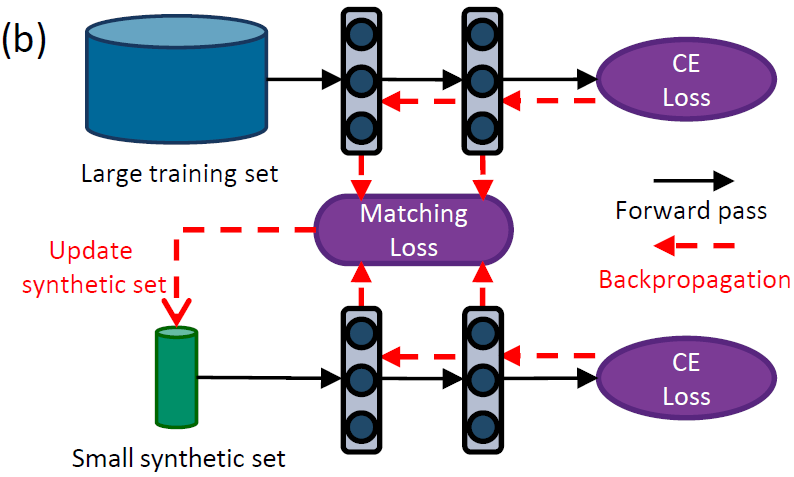
后续有不少学者在损失函数$Loss$上做文章,如不仅关心方向,还关心大小(欧式距离)等,此处就不再赘述了。
Multi-Step Parameter Matching
有一步梯度匹配,就会有多步梯度匹配。Multi-Step Parameter Matching最先在Dataset Distillation by Matching Training Trajectories中被Cazenavette et al.提出,一般简称MTT。在Kernel Ridge Regression Based Methods出现之前,这是表现最好的方法。其本质上是对Single-Step的一种优化,因为单步的匹配本质上是一种贪心的算法,它不一定能够得到全局的最优,而用训练集的多步梯度下降来匹配Synthetic Data的一步或两步梯度下降能够为更新Synthetic Data带来更加全局的、稳定的优化路径。方法示意图如下:
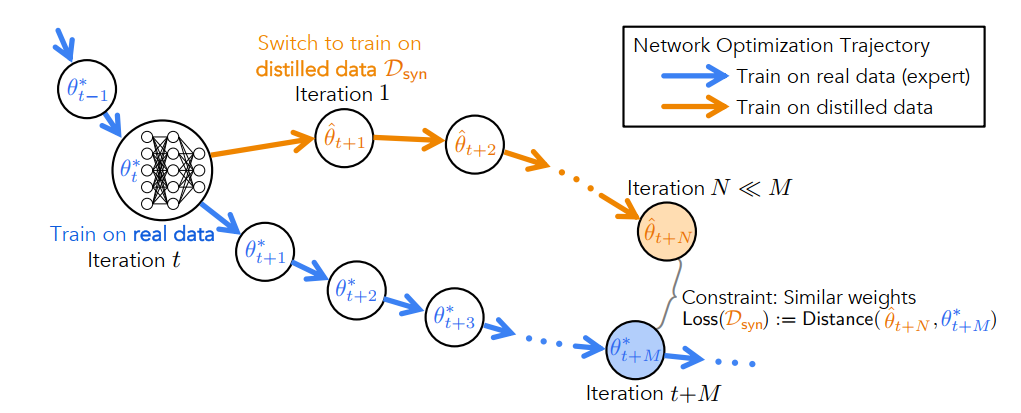
此外,文中用到的损失函数也不同,作者使用的损失函数是规范化了的欧式距离(的平方):
$$
Loss(\mathcal{S},\mathcal{T})=\frac{||\theta ^{\mathcal{S}} _{t+N}-\theta ^{\mathcal{T}} _{t+M}||^2 _2}{||\theta ^{\mathcal{T}} _{t}-\theta ^{\mathcal{T}} _{t+M}||^2 _2}
$$
MTT的另一大优点是蒸馏速度很快,因为其训练集训练的网络都是预先训练好的,这些预训练好的网络被称为buffer或者teacher net。后续也有不少的学者对MTT进行了优化,如:
- FTD:优化了buffer,使得生成的buffer能够提供更接近于Synthetic Data训练网络的优化路径;
- DDPP:优化了更新Synthetic Data的时机,即预先评估本次更新Synthetic Data能够带来的收益,根据收益大小来决定是否要执行本次更新。评估的方式是为$\theta ^{\mathcal{T}} _{t+M}/\theta ^{\mathcal{S}} _{t+N}$设置一个阈值$\epsilon$,当两者的比例小于该阈值时就不执行本次Synthetic Data的更新。
- ...
Distribution Matching
Distribution Matching,分布匹配,核心思想是让Synthetic Data的统计分布尽可能地接近训练集。接近程度的衡量指标一般用的是Maximum Mean Discrepancy(MMD),即用高阶矩来衡量两个分布的接近程度,而高级矩的计算则常以通过神经网络将输入特征映射到高维空间后,计算高维空间向量距离的方式进行。这种方法最大的优点就是蒸馏速度很快。
Single Layer Distribution Matching
该方法是分布匹配最初的方法,由Zhao et al.在Dataset Condensation with Distribution Matching提出,一般简称DM。思路与前文提到的一致。其计算高阶矩所采用的神经网络是原来用于分类任务的神经网络,不过去掉了softmax操作。基本流程为:
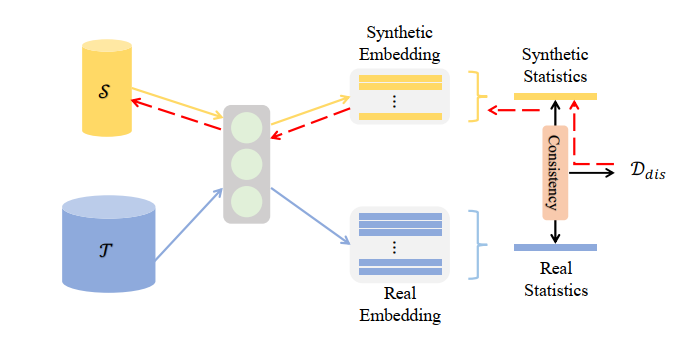
Multi Layer Distribution Matching
该方法由Wang et al.在Cafe: Learning to condense dataset by aligning features上提出,一般简称CAFE。实际上是对DM的优化,主要的不同点在于:DM只对整个神经网络的输出向量进行匹配,而CAFE则是对每一个隐藏层的输出向量进行匹配并相加。本质上差不多,没有跳出Distribution Matching的框架。