Computational Complexity Space Complexity 1
Space Bounded Computation:空间边界的计算
空间是计算资源,是可重用的。研究空间复杂度,只考虑只有一条带子的图灵机即可。
空间复杂性(函数)的定义:对函数$S: \mathbf{N}\to \mathbf{N}$和语言$L \in \{0,1\} ^ *$,如果存在常数$c$和图灵机$\mathbb{M}$能使用不超过$cS(n)$的非空工作带格子判定输入长度为$n$的$L$,就称$L \in \textbf{SPACE}(S(n))$。
不计算输入所占用的格子。空间可构造和完全空间可构造完全类比时间可构造和完全时间可构造。
对非确定图灵机,$L \in \textbf{NSPACE}((S(n)))$当且仅当每条路径上使用的非空工作带格子都不超过$cS(n)$。
Configuration Graph:格局图
- $C _{\text{start}}$:初始格局;
- $C _{\text{accept}}$:接受格局,图灵机中止且带子上的结果为1。
格局图:一个图灵机$\mathbb{M}$的格局图$G _{\mathbb{M},x}$是一个有向图,它的结点是某个格局$C$,边是一次计算。若使用格局图,则$\mathbb{M}$接受$x$当且仅当在格局图$G _{\mathbb{M},x}$上存在从$C _{\text{start}}$到$C _{\text{accept}}$的路径。
Size of Configuration Graph:格局图的大小
对于一个时间复杂度为$S(n)$的图灵机$\mathbb{M}$,由于只考虑一条工作带,因此,某个长度为$n$输入$x$,其某一步的格局可用$O(S(n))个$比特编码。因此,整个格局图的结点个数就是$2 ^{O(S(n))}$。
当我们想要判断某两个结点间是否存在边时,我们只需要判断某两个格局$C _1$和$C _2$是否存在一步到达的关系,即看能否通过仅修改某个格局$C _1$编码的$1$个bit和表示读写头的几个bit,就让$C _1=C _2$。不难看出,该算法的时间复杂度是$O(S(n))$,空间复杂度是$O(\log S(n))$,因为我们只需要按位比较,并记录位置的编码即可,而$O(S(n))$个位置可用$O(\log S(n))$的二进制串表示。
但要求$C _1$和$C _2$交叉输入,否则带头的来回移动会让时间复杂度为平方。
Space vs Time
设空间函数$S(n)$是空间可构造的,则:
$$
\textbf{TIME}(S(n))\subseteq \textbf{SPACE}(S(n))\subseteq \textbf{NSPACE}(S(n))\subseteq \textbf{TIME}(2 ^{O(S(n))})
$$
第一个包含关系:一步最多多用一个格子;
第二个包含关系:确定是非确定的特例;
第三个包含关系:判定一个非确定图灵机能否在$O(S(n))$的空间内判定每个问题,等价于验证格局图中是否存在由$C _\text{start}$到$C _{\text{accept}}$的路径,而这可通过BFS在多项式时间复杂度内完成。格局图中总结点数为$2 ^{O(S(n))}$,因此第三个包含关系成立。
注意:以上相互包含的都是问题集合,如第一个包含关系意为:时间复杂度为$S(n)$的问题是空间复杂度为$S(n)$问题的子集。
对所有的空间可构造的$S(n)$,$\textbf{TIME}(S(n))\subseteq \textbf{SPACE}(S(n)/ \log S(n))$
Space Complexity Class
- $\textbf{L}$类:$\textbf{SPACE}(\log (n))$
- $\textbf{NL}$类:$\textbf{NSPACE}(\log (n))$
- $\textbf{PSPACE}$类:$\bigcup _{c>0} \textbf{SPACE}(n ^c)$
- $\textbf{NPSPACE}$类:$\bigcup _{c>0} \textbf{NSPACE}(n ^c)$
$$
\textbf{NP}\subseteq \textbf{PSPACE}
$$
上式成立是因为空间是可以重复利用的,故我们可以用相同的空间在多项式时间内(空间)验证不同的路径是否成立。
PATH is in NL
$\text{PATH}=\{<G,s,t>\}$定义为判断在图$G$中是否存在从$s$到$t$的路径。
$$\text{PATH}\in \textbf{NL}$$
这是因为:在有$n$个结点的图中,不考虑重复边,$s$到$t$的最长路径长度为$n-1$。因此,我们总可以不断地从$s$做$n-1$次猜测,每次猜测选择一个邻居,走到邻居,并继续猜测。总会有那么一个猜测路径,使得我们可以到达$t$(若$s$和$t$之间确实存在路径)。这一过程中,我们需要记录当前结点,而当前结点可用$\log n$的空间编码,还要记录步数,而步数可用$\log (n-1)$的空间编码,又因为空间是可以重用的,所以总的空间复杂度为$O(\log n)$。
对空间复杂度为$S(n)$的图灵机,通用图灵机模拟它的空间复杂度为$O(S(n))$。
Space Hierarchy Theorem:空间谱系定理
若$f$和$g$都是空间可构造的,且$f(n)=o(g(n))$,则:
$$
\textbf{SPACE}(f(n)) \subsetneq \textbf{SPACE}(g(n))
$$
证明类似时间谱系定理。
Logspace Reduction:对数空间归约
隐式对数空间可计算(Implicitly Logspacec Computable)函数$f:\{0,1\} ^ *\to \{0,1\} ^ *$满足如下三个性质:
- 输出长度有限:$\exists c,\forall x,|f(x)|\le c |x| ^c$
- 输出长度可在对数空间内计算:$\{<x,i>|i \le |f(x)|\}\in L$
- 输出结果可确定:$\{<x,i>|f(x) _i = 1\}\in L$
以上三个性质的推断都依赖于前一个性质。如果存在这么一个函数$f$,使得对于问题$B$和问题$C$,$x\in B$当且仅当$f(x) \in C$,那么我们称$B$是可在对数空间归约于$C$的,即$B \le _L C$。
$f(x)$作为$C$的输入,是不能被直接写到$C$的输入带上的,因为$f(x)$的长度是多项式的。不过,$f(x)$的三个性质使得图灵机可以在对数空间内计算出$f(x)$任意位置的值,由于空间的可重用性,输入$f(x)$实际只用了对数空间(每次一位一位地输入)。
$B$对数空间归约到$C$,说明在不消耗更多空间资源的情况下,$C$是更复杂的问题。
对数空间归约具有传递性,即,若$B \le _L C$,$C \le _L D$,则$B \le _L D$。证明:
- $B \le _L C$,所以对$x \in B$,可在对数空间$O(\log |x|)$内计算$f(x)$。
- $C \le _L D$,所以对$f(x) \in C$,可在对数空间$O(\log |f(x)|)$内计算$g(f(x))$。
- 又由于空间的可重复利用性,用于计算$f(x)$的对数空间可被重复用于计算$g(f(x))$,因此$O(\log |f(x)|)=O(\log |x|)$。
$\text{PSPACE}$ Completeness
空间完备性(Space Completeness):如果$\forall L \in \textbf{PSPACE}$,$L \le _L L'$,则称语言$L'$是$\textbf{PSPACE}-\text{hard}$的。如果进一步地,$L ' \in \textbf{PSPACE}$,则称语言$L'$是$\textbf{PSPACE}-\text{complete}$的。某个完备的(Complete)语言是这个空间复杂性类中最难的语言/问题。
Quantified Boolen Formula
量化布尔公式(Quantified Boolen Formula,QBF)被定义为这样的式子:
$$
Q _1 x _1 Q _2 x _2...Q _n x _n.\space \phi(x _1,...,x _n)
$$
其中,$Q _i$是量词(Quantifier),要么是$\forall$,要么是$\exists$;$x _i$是布尔值,要么是$0$,要么是$1$;$\phi$是不包含$x _1,...,x _n$以外的任何自由变量的布尔公式,该公式要么为$\text{True}$,要么为$\text{False}$,如:
$$
\forall x,\exists y,x=y
$$
显然,上述公式值为$True$。
空间复杂度两个原则:格局图、深度优先
Stockmeyer-Meyer Theorem
定理:TQBF是$\textbf{PSPACE}-\text{complete}$的。定理中,$\text{TQBF}$是所有值为$\text{True}$的QBF集合。定理的证明如下:
要证明上述定理,即要证明$\forall L \in \textbf{PSPACE}$,$L \le _L $TQBF,且TQBF$\in \textbf{PSPACE}$。
1.TQBF$\in \textbf{PSPACE}$
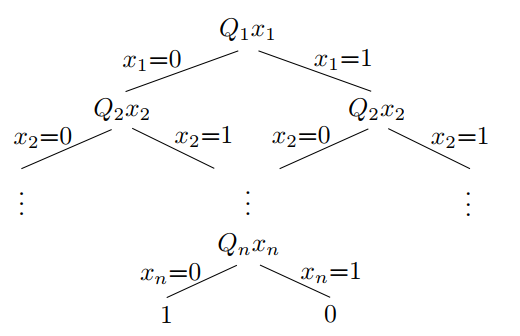
假定某个QBF为$\psi = Q _1 x _1 Q _2 x _2...Q _n x _n.\space \phi(x _1,...,x _n)$,由于$x _i$只有两种取值可能,因此我们可以将$\psi$所有可能的形式表示为一棵二叉树:
Fig. 1. QBF
对该二叉树使用一次深度优先遍历(实际上应该使用后序遍历)即可判定该问题。DFS过程中,我们可以自下而上求出所有非叶子结点的值,最终根结点的值就是QBF的判定结果,整个过程中,我们最多需要记录$n$个祖先,因而该算法的空间复杂度实际上为$O(n)$。因此TQBF$\in \textbf{PSPACE}$。证毕。
2.$\forall L \in \textbf{PSPACE}$,$L \le _L $TQBF
$L \in \textbf{PSPACE}$说明存在图灵机$\mathbb{M}$,对输入$x \in L$,它能在多项式空间内输出$\mathbb{M}(x)=1$以及格局图中存在$C _{\text{start}}$到$C _{\text{accept}}$的路径。
要证明条件2,我们只需要证明对$x \in L$,存在$\phi(x)\in $TQBF。不妨令$\phi(x)=\psi _i (C,C')$,其中,当格局$C$和$C'$之间存在长度不超过$2 ^i$的路径时$\psi _i (C,C')=1$。
对于$\psi _i (C,C')$,若其值为$1$,则在$C$和$C'$之间一定存在一个格局$C''$,它到这两个格局的路径长度不超过$2 ^{i - 1}$,因此$\psi _i (C,C')$就可以被转换为$\psi _{i-1} (C,C'') \lor \psi _{i-1} (C',C'')$。该问题可被表示为:
$$
\exists C'' \forall D ^1 \forall D ^2.((D ^1=C \land D ^2 =C'))\lor ((D ^1=C'' \land D ^2 =C)) \rightarrow \psi _{i-1}(D ^1, D ^2)
$$
只要我们能够判断上面前蕴含后的关系成立,则$\psi _i (C,C')=1$成立。判别上式的空间复杂度为$|\psi _i|=|\psi _{i-1}(D ^1, D ^2)|+cS(|x|)$,其中,后一项是用于记录箭头前的格局的空间(每个格局空间复杂度$S(|x|)$)。那么对于空间复杂度为$S(|x|)$的$L$,它的格局图中最多有$2 ^{S(|x|)}$个结点,于是判断$L$,就可以转为判断$\psi _{S(|x|)}$,即判断QBF$\phi (x)$。$|\phi (x)|=|\psi _{S(|x|)}|=O(S(|x|) ^2)$,多项式的平方仍然是多项式,所以$x\in L$,$\phi (x) \in $TQBF,证毕。前面的式子能成立是因为最终$\psi _{S(|x|)}$会被转化为$\psi _{1}$,期间会多出$S(|x|)$个$c S(|x|)$。
Savitch Theorem
定理:如果$S$是空间可构造的,那么$\textbf{NSPACE}(S(n)) \subseteq \textbf{SPACE}(S(n) ^2)$。证明如下:
该定理的证明与上面的条件2证明几乎一致。对于空间复杂度为$S(n)$的非确定图灵机$\mathbb{N}$,它可以在$S(n)$的空间内判定$L$,其格局图的大小为$2 ^{S(n)}$。很自然地,判定$L$可以被转换为判定格局图中是否存在$C _{\text{start}}$到$C _{\text{accept}}$的路径。该问题可以被$\phi (x)$在$c S(n) ^2$空间内解决。所以$\textbf{NSPACE}(S(n)) \subseteq \textbf{SPACE}(S(n) ^2)$。证毕。
由于多项式的平方还是多项式,所以由上述定理,我们可以得到:
$$
\textbf{NPSPACE} \subseteq\textbf{PSPACE}
$$
又因为确定图灵机是非确定图灵机的特例:
$$
\textbf{PSPACE} \subseteq \textbf{NPSPACE}
$$
所以:
$$
\textbf{PSPACE} = \textbf{NPSPACE}
$$
NL Completeness
如果$C \in \textbf{NL}$,且对$\forall B \in \textbf{NL}$,$B \le _L C$,则$C$是$\textbf{NL}-$ complete。
定理:$\text{PATH}$是$\textbf{NL}$完全的。证明如下:
由于前面已经证明$\text{PATH} \in \textbf{NL}$,所以要证明上述结论,即要证明对$\forall L \in \textbf{NL}$,$L \le _L \text{PATH}$,即要证明$\forall x \in L$,$\exists f$,$f(x) \in \text{PATH}$。
与前面的证明类似,对在$\log(n)$空间内判定$L$的非确定图灵机$\mathbb{N}$,设其输入为$x$,则该问题可以被转换为在格局图$G _{\mathbb{N},x}$中判断$C _\text{start}$和$C _\text{accept}$间是否存在路径,即:
$$
x \to < G _{\mathbb{N},x},C _\text{start},C _\text{accept} >
$$
由于$\mathbb{N}$的空间复杂度是$\log (n)$,所以格局图中的每一个格局都可以用$\log (n)$的bit编码,且共有多项式个格局(顶点)。用邻接矩阵$A$表示格局图$G _{\mathbb{N},x}$的结构关系,由于各个顶点的编码长度为$\log (n)$,所以任意两个顶点的一步可达性可在对数空间内判定,又由于空间的可重复利用性,整个邻接矩阵可以在对数空间内被构造出来,而起始格局和终止格局都是固定的$01$串,所以$< G _{\mathbb{N},x},C _\text{start},C _\text{accept} >$可以在对数空间内被构造出来,而$< G _{\mathbb{N},x},C _\text{start},C _\text{accept} > \in \text{PATH}$,所以$L \le _L \text{PATH}$。证毕。
有向无环图的$\text{PATH}$问题也是$\textbf{NL}$完全的。
Immerman-Szelepcsenyi Theorem
补类(补问题):一个类的补类指在所有类中刨去改类后剩下的类,如,对$\textbf{T}$类,其补类记为$\text{co}\textbf{T}$或$\overline{\textbf{T}}$,定义为:
$$
\text{co}\textbf{T}=\overline{\textbf{T}}=\{\{0,1 ^*\}-L \in \textbf{T}\}
$$
一个有趣的结论:
$$
\begin{align*}
\text{co}\textbf{NPSPACE}
&=\overline{\textbf{NPSPACE}} \\
&=\overline{\textbf{PSPACE}}\\
&=\textbf{PSPACE}\\
&=\textbf{NPSPACE}
\end{align*}
$$
定理:$\overline{\text{PATH}}\in \textbf{NL}$。$\overline{\text{PATH}}$的含义为:从$A$出发到不了$B$。的证明如下:
???????
由上述定理,我们可以得到$\overline{\textbf{NL}}= \textbf{NL}$:
$A \le _L B$,则$\overline{A} \le _L \overline{B}$
因为$L \le _L \text{PATH}$,所以$\overline{L} \le _L \overline{\text{PATH}}$,所以$\overline{\text{PATH}}$是$\overline{\textbf{NL}}$完全的,而$\overline{\text{PATH}}\in \textbf{NL}$,所以$\overline{\textbf{NL}}= \textbf{NL}$。
事实上,对$\forall S(n) \ge \log (n)$,若$S(n)$时间可构造,则:
$$
\overline{\textbf{NSPACE}(S(n))}=\textbf{NSPACE}(S(n))
$$
$$
\textbf{L}\subseteq \textbf{NL}\subseteq \textbf{P}\subseteq \textbf{NP}\subseteq \textbf{PSPACE}\subseteq \textbf{EXP}
$$