Computational Complexity: Polynomial Hierarchy

Posted on Edited on In Views: Word count in article: 668 Reading time ≈ 2 mins.
本篇是计算复杂性（CS7313）的第四章，主要研究多项式谱系问题。

Problem Beyond NP

$\textbf{MINIMAL}=\{\phi | \phi \text{DNF} \land \forall \text{DNF}\psi. |\psi| < |\phi| \to \exists u. !{(\psi(u) <=>\phi(u))}\}$，即$\phi$是所有等价的析取范式中最短的。

Meyer-Stockmeyer's Definition

$$
\begin{align*}
\Sigma _0 ^p &=\textbf{P}\\
\Sigma _{i+1} ^p &=\textbf{NP} ^{\Sigma _{i} ^p}\\
\Delta _{i+1} ^{p}&=\textbf{P} ^{\Sigma _{i} ^p} \\
\Pi _i ^p &= \textbf{co-}\Sigma _{i} ^p
\end{align*}
$$

有：

  • $\Sigma _{i} ^p \subseteq \Delta _{i+1} ^{p} \subseteq \Sigma _{i + 1} ^p$
  • $\Pi _i ^p \subseteq \Delta _{i+1} ^{p} \subseteq \Pi _{i + 1} ^p$

其中第二项是对第一项的取补。

定义多项式谱系为：$\textbf{PH}=\bigcup _{i \ge 0}\Sigma _i ^p=\bigcup _{i \ge 0}\Pi _i ^p=\bigcup _{i \ge 0}\Delta _{i+1} ^p$。

某个语言$L \in \Sigma _i ^p$或$L \in \Pi _i ^p$的证据：

  • 对$\Sigma _i ^p$，证据为$\exists u _1 \in \{0,1\} ^{q(|x|)}.\forall u _2 \in \{0,1\} ^{q (|x|)}...Q _i u _i \in \{0,1\} ^{q (|x|)}$
  • 对$\Pi _i ^p$，证据为$\forall u _1 \in \{0,1\} ^{q(|x|)}.\exists u _2 \in \{0,1\} ^{q (|x|)}...Q _i u _i \in \{0,1\} ^{q (|x|)}$

这两个是对偶问题，只需证第一个即可。

  • 从右到左：猜测一个$u _1$，对每个猜测，计算$\Pi _{i-1} ^P$，而于是所有的猜测就是$\textbf{NP} ^{\Pi _{i-1} ^P}=\textbf{NP} ^{\Sigma _{i-1} ^P}=\Sigma _{i} ^P$。
  • 从左到右：Cook-Levin定理，转化为$\textbf{SAT}$，再把$\textbf{SAT}$转化为量词的交替。

$\Sigma _i \textbf{SAT}$是$\Sigma _i ^p$中最难的问题，即它是$\Sigma _i ^p$完全的。证明：将$\mathbb{M}(x,u _1,...,u _{i+1})$Cook-Levin归约到$\Sigma _i \textbf{SAT}$。

因为$\Sigma _i \textbf{SAT} \subseteq \textbf{PSPACE}$，所以$\textbf{PH} \subseteq \textbf{PSPACE}$

Alternating Turing Machine

交替图灵机：非确定图灵机的推广，每个状态都被标注为$\{\exists,\forall,\text{halt}\}$之一。交替图灵机$\text{ATM}$接受$x$当且仅当交替图灵机的执行序列中存在一个接受子树。

接受子树：所有叶子结点标记$\text{halt}$且均为$1$，若某个非叶子结点被标记为$\exists$则它只有一个孩子在接受子树中，若被标记为$\forall$则有两个孩子接受子树中。

$\text{TQBF}$可用$\text{ATM}$在平方时间和线性空间判定。

  • $\textbf{NSPACE}(S(n)) \subseteq \textbf{ATIME}(S ^2 (n))$：格局图、路径，$\exists$则猜测，$forall$则并行计算，共猜测$S$次，每次耗时$S$。
  • $\textbf{ATIME}(T(n)) \subseteq \textbf{SPACE}(T (n))$：DFS。
  • $\textbf{ASPACE}(S(n)) \subseteq \bigcup _ {c \ge 0}\textbf{TIME}(c ^{S(n)})$：格局图，枚举。
  • $\textbf{TIME}(T(n)) \subseteq \textbf{ASPACE}(\log T(n))$：Cook-Levin证明一的图从下往上，猜测$\exist$，并行地验证$\forall$。每条路径空间为对数空间。

1

Fig. 1.

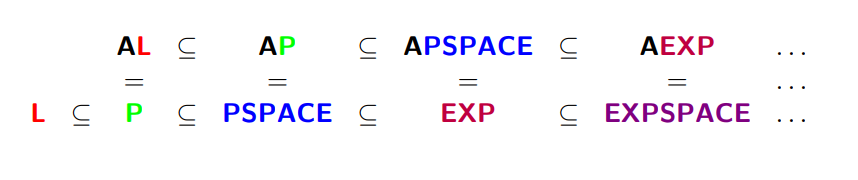
无穷谱系猜测是比$\textbf{NP}=\textbf{P}$更强的假设，它假设多项式谱系间存在严格的包含关系。