VAE

Intuitive: AE和VAE

Fig. 1. AE, VAE

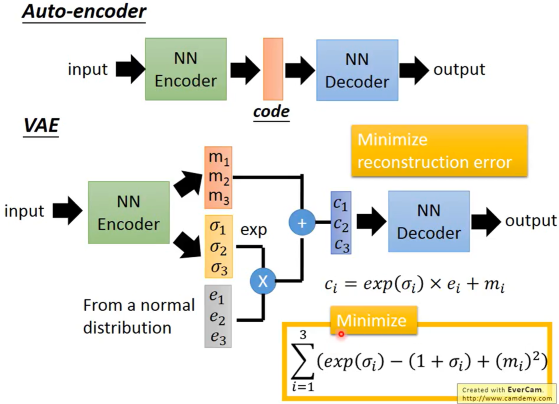
训练时，两者都是优化输入图片和输出图片的差距来更新参数。最后部署、生成图片时，只使用Decoder，接受某个向量输入，生成图片。

AE的Encoder本质上是将一个图片映射为高维向量空间的一个点，而VAE的Encoder通过加入随机噪声，使得图片被映射为高维空间的一段区间。这样的好处在于，当输入Decoder的向量介于某两个向量之间时，VAE更有可能输出一个结合了这两个向量对应图片特征的图片，因为训练的误差会诱导网络这么做。

Fig. 2. Intuitive. AE, VAE

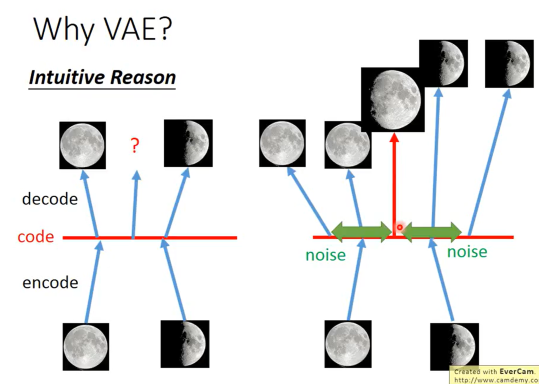
原理: 噪声角度

VAE的Encoder输出两个向量，一个原始编码$m$ (均值)，一个方差$\sigma$。我们期望加了噪声后的分布能尽可能地趋近于一个正态分布，因此引入一个从正态分布中采样出的向量$e$引导噪声。$\sigma$和$e$结合生成最终的噪声。但是，极端情况为学到的$\sigma$趋近于负无穷，使得VAE退化为AE。因此，除了输入图片和输出图片产生的$\mathcal{L} _1$以外，引入$\mathcal{L} _2$:

$$
\mathcal{L} _2 = \min\sum (\text{exp}(\sigma _i)-(1+\sigma _i) + m _i ^2)
$$

其中前两项在$\sigma _i$取0时取最小值，这将迫使$\sigma _i$能够产生有效的噪声。最后一项是L2正则。

原理: 高斯混合模型角度

对于一个给定的图片集，其在高维空间服从一个高斯混合分布$P(x)$ ($x$是图的RGB矩阵)，$P(x)$的值表明某个$x$属于这个空间的概率 (如某张图片是宝可梦精灵的概率)。

Fig. 3. GMM

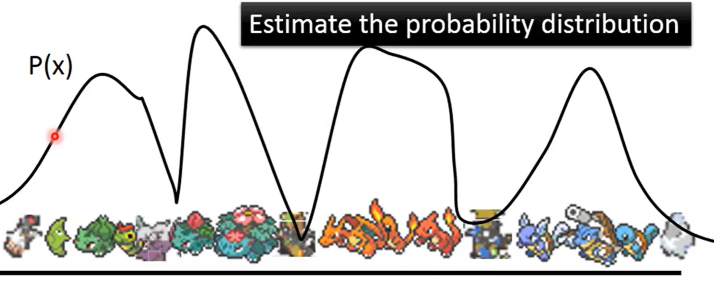
高斯混合模型由多个高斯分布组成，因而可写成:

$$
P(x)=\sum _m P(m)P(x | m)
$$

其中$P(m)$是$m$高斯分布在混合分布中的权重。$P(x|m)$即为$m$高斯分布，有均值$\mu _m$和方差$\sigma _m$。极限情况下，高斯混合模型由无数个高斯分布组成:

$$
P(x) = \int _z P(z)P(x |z)dz
$$

假设$z$服从一个标准正态分布，要将$z$对应为一个高斯分布，只需要生成均值$\mu(z)$和方差$\sigma (z)$即可:

Fig. 4. Decoder

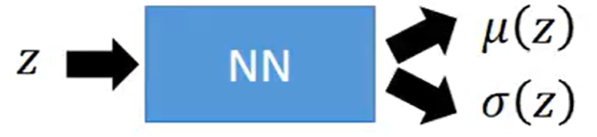
生成这样映射的过程显然是一个参数估计的过程，可由最大似然估计 (MLE) 优化:

$$
L = \max\sum _x \log P(x)
$$

这又可以转化为一个EM过程。$z$是一个隐变量，可由已知的$x$估计，对$\log P(x)$做如下修改:

$$
\log P(x) = \int _z q(z|x)\log P(x)dz
$$

$q(z|x)$是给定$x$，$z$的概率密度，显然其积分为1，故上式是一个恒等式。进一步处理:

$$
\begin{align*}
\log P(x) =&\int _z q(z|x)\log (\frac{P(z,x)}{P(z|x)})dz\\
=&\int _z q(z|x)\log (\frac{P(z,x)}{P(z|x)}\frac{q(z|x)}{q(z|x)})dz\\
=&\int _z q(z|x)\log (\frac{P(z,x)}{q(z|x)})dz+\int _z q(z|x)\log (\frac{q(z|x)}{P(z|x)})dz
\end{align*}
$$

第一步用的是条件概率密度，其他都是普通的变换。第二项被称为KL散度 ($\text{KL}(q(z|x)||P(z|x))$)，用于衡量两个分布的相似性，大于0。故

$$
\log P(x) \ge L _b=\int _z q(z|x)\log (\frac{P(z,x)}{q(z|x)})dz
$$

这一步体现了引入$q(z|x)$的作用。$q(z|x)$的值不会影响$L$ (积分恒为1)，但是通过优化$q(z|x)$，使其趋近于$P(z|x)$，我们可以让KL散度项逐渐趋于0，使得:

$$
\log P(x) \approx L _b
$$

于是MLE的优化对象就变为$L _b$，而$L _b$可进一步转化为:

$$
\begin{align*}
L _b=&\int _z q(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)})dz\\
=&\int _z q(z|x)\log (\frac{P(z)}{q(z|x)})dz +\int _z q(z|x)\log (P(x|z))dz
\end{align*}
$$

其中前项是$P(z)$和$q(z|x)$的KL散度的相反数。而$q(z|x)$由$x$经过映射生成:

Fig. 5. Encoder

这项实际上就是VAE的$\mathcal{L} _2$，因为要$\max L _b$，则必须要$\min \text{KL}(P(z),q(z|x))$，也就是要让生成的编码尽可能地趋向正态分布。

而第二项实际上是在求$\log P(x|z)$在分布$q(z|x)$下的均值:

$$
\int _z q(z|x)\log (P(x|z))dz=E _{q(z|x)}[\log P(x|z)]
$$

$P(x|z)$又由$z$经过映射生成。最终便可整合为VAE的过程:

Fig. 6. VAE

即$x$生成$q(z|x)$高斯分布，然后从中采样出$z$，$z$生成高斯分布$P(x|z)$，由于均值$\mu (x)$处的概率最大，因此$x$越趋近$\mu (x)$，概率就越大，这也就是$\mathcal{L} _1$。

Conditional VAE

在训练时给VAE一些引导，使其Encoder的生成有倾向性。可用于文本生成图片。

Shortcoming of VAE

只是对训练集的模仿。

Reference

台湾大学李宏毅课程。