LLM

基础知识

Entropy & Cross-entropy & KL Divergence & Perplexity

对于随机事件 $X$, 其有 $n$ 种可能的具体事件, 每个具体事件发生的概率为 $p(x _i)$. 从信息论的角度, 当我们观测到具体事件时, 该具体事件所蕴含的信息量 $H(x _i)$ 应满足:

1. 越小概率的事件发生了产生的信息量越大, 即事件的包含的信息量与其发生的概率成反比;
2. 两个独立随机事件同时发生时, 其产生的信息量应等于两者分别发生时产生信息量的和, 即 $H(x _i\cdot y _j)=H(x _i) + H(y _j)$.

$-\log(x)$ 函数正好满足这一性质. 因此 $-\log(x _i)$ 即表示具体事件 $x _i$ 发生时产生的信息量. 当以 2 作为底数时, 其又可被解释为"表征所这一信息需要的比特数". 对于整个随机事件 $X$, 其信息量的期望即为该随机事件 $X$ 的 信息熵 (简称熵, Entropy):

$$
Entropy=H(p, X)=-\sum\limits _{i=0}^{n-1}p(x _i)\log p(x _i)
$$

熵同时也代表着系统的混乱程度, 当我们不得不用近似的随即事件分布 $q$ 去拟合真实的随机事件分布 $p$ 时, 其熵的期望称为交叉熵 (Cross-entropy):

$$
Cross-entropy=H(p, q, X)=-\sum\limits _{i=0}^{n-1}p(x _i)\log q(x _i), H(p, q, X) \ge H(p, X)
$$

真实熵与交叉熵的差距即 KL散度 (Kullback–Leibler Divergence)：

$$
D _{KL}(p||q)=H(p, q, X)-H(p, X)=-\sum\limits _{i=0}^{n-1}p(x _i)\log\frac{q(x _i)}{p(x _i)}=\sum\limits _{i=0}^{n-1}p(x _i)\log\frac{p(x _i)}{q(x _i)}=\mathbb{E} _{x\sim p}\log\frac{p(x _i)}{q(x _i)}
$$

KL散度衡量了真实分布和近似分布的差距但不是距离, 因为 $KL(p, q) != KL (q, p)$, 除非两个分布完全一样.

困惑度 (Perplexity) 是熵 (或交叉熵) 的指数, 取决于不同的场景, 对概率分布来说, 指熵的指数; 对模型来说, 指交叉熵的指数 (即 loss 的指数).

问答

1. 为什么分类问题用 Cross-entropy 而不用 MSE?

从损失函数自身来说, CE 是有倾向性的, 因为我们只对 Label 会有熵, 因此 CE 就倾向于优化 Label 的概率趋近于1; 而 MSE 是没有倾向性的, 比如对于 [1, 0, 0] 这个 Label, MSE 会认为 [0.8, 0.1, 0.1] 比 [0.8, 0.15, 0.1] 好, 即平均会比有倾向性好, 但对于分类来说这样是没有必要的; 然后从梯度的传递来说, 对 softmax 后的 MSE 来说, 其梯度是 $(-y _{hat}(1-y _{hat})^2)$, 这会导致其在我们分类完全错误或正确的时候没有梯度, 而越是分类错误我们反而越需要梯度, CE 则避免了这个问题, 因为它的梯度是 $y _{hat}-1$, 即在分类错误的时候会有最大的梯度.

2. Label Smoothing 公式以及作用原理?

one-hot 编码时 softmax 后交叉熵梯度为零时的理论情况为: $y _{hat}-y$, 即此时正确类 softmax 后的概率为 1, 相应地, 错误类的概率都为 0, 进而可推导出来正确类的 logit 是一个常数, 而错误类的 logit 是负无穷. 这样会导致正确类和错误类的logit输出误差很大, 网络的泛化能力不强. 并且因为网络训练时会有一些正则化的存在, logit的输出很难是负无穷. label smoothing 的编码方式只要正确类和错误类有一定的数值误差即可，这个取决于分类的类别数量和 $\epsilon$. 网络极使在正则化的情况下也比one-hot容易学习到最优情况.:

$$
y _i=
\begin{cases}
1-\epsilon, i=true,\
\frac{\epsilon}{K-1}, otherwise, \text{K is the number of class}
\end{cases}
$$

# code implementation
# (B, T, V)
logits = model(...)
log_probs = -F.log_softmax(logits, dim=-1)

# (B, T, V) -> (B, T), 相当于给其他的 label 均分了一些数值
ce_loss = log_probs.gather(dim=-1, index=labels)
smoothed_loss = log_probs.sum(dim=-1) / V

loss = (1 - epsilon) * ce_loss + epsilon * smoothed_loss

3. top-k、top-p, beam search

top-k: 选取前 k 个概率最高的词, 将这 k 个词的概率重新归一化形成新的分布, 从新的分布中随机采样; top-p: 选取累计概率超过 p 的词集 S, 在 S 中进行随机采样, 比 top-k 更灵活; beam-search: 与前两者不同, 最终会生成 B 个候选序列, 每次生成, 选取概率最高的 B 个词, 然后用这 B 个词独立接着生成, 重复上述过程 (注: 第一步以后, 是所有的生成结果中选 B 个), 最终得到 B 个生成结果.

def beam_search(decoder, k, max_time_steps):
    sequences = [[['<start>'], 1.0]]
    ret = []

    while k and max_time_steps:
        all_candidates = []
        for sequence in sequences:
            seq, score = sequence[0], sequence[1]
            token_list, scores = decoder(seq)
            for token, s in zip(token_list, score):
                candidate = [seq + token, score * s]
                all_candidates.append(candidate)
        # 是在所有的生成结果中选前 k 个, 而不是每条分支选 k 个
        ordered = sorted(all_candidates, key=lambda tup: tup[1])  # 按 score 升序排序
        sequences = ordered[-k:]  # 选分数最高的 k 个
        tmp = []
        for seq in sequences:
            if seq[0][-1] == '<end>':
                ret.append(seq)
                k -= 1
            else:
                tmp.append(seq)
        sequences = tmp
        max_time_steps -= 1
    if len(ret) < k:
        ret.append(sequences[0])
    return ret

4. accuracy, precision, recall, roc, auc

Acc: (TP + TN) / (TP + FP + TN + FN), 判断正确的比例; Precision: (TP) / (TP + FP), 预测为正类的中真正正类的比率; Recall: (TP) / (TP + FN), 真正为正类样本被预测正确的比例. 记忆方法: y(预)p z(真)r. F1 score 是 PR 的调和平均值. ROC: 二分类下, 正类被预测正确的准确率 (Y 轴) 和负类被预测为正类的比例 (X 轴) 随阈值的分布. ROC 下的面积为 AUC, 越大表模型分类效果越好.

5. ROC 和 AUC 的进一步讨论

AUC 一种直观的解释是给定一个正负样本对, 模型对正样本打分高于负样本的概率, 因此 AUC 很适合作为排序场景的指标 (如用户是否会点击、是否会购买等). 也正因如此, AUC 对正负样本的比例不敏感, 因为 AUC 是对正负样本分别考虑的, 是一个相对客观地分别评估模型在正样本和负样本中能力的指标, 只要正负样本自身的分布不发生大的变化, 两者的比例对 AUC 几乎没影响. 同样地, 由于这个性质, AUC 只考虑相对性, 当场景需要考虑绝对数量的时候, 即场景需要正例的概率很高时, AUC 可能不太合适, 如广告, 此时logloss可能更适合. 实际上就是 Bradley-Terry (对 ROC 的近似) 和 CE loss. AUC 有三种计算方法：1）取定不同阈值画图；2）正样本大于负样本的概率，太慢；3）对二的改进，即先排序。

import torch

def BCE(self, target):
    loss = (target - 1) * torch.log(1-self) - target * torch.log(self)
    return loss.mean()

label = torch.randint(low=0, high=2, size=(10,), dtype=torch.float32)
y = torch.nn.functional.sigmoid(torch.rand((10,)))

print(BCE(y, label))
print(torch.nn.functional.binary_cross_entropy(y, label))

def CE(self, target):
    self = torch.nn.functional.softmax(self, dim=-1)
    loss = -torch.log(torch.gather(self, dim=1, index=target.unsqueeze(-1)))
    return loss.mean()

label = torch.randint(low=0, high=5, size=(10,))
y = torch.rand((10, 5))
loss = torch.nn.CrossEntropyLoss()
print(CE(y, label))
print(loss(y, label))

6. softmax 温度系数的影响

温度系数大于 1 时, 会软化分布, 使得输出的分布更加平滑; 温度系数小于 1 时, 输出的概率分布会更加接近 one-hot 的形式, 模型对结果的置信度会更高, 所以在推理的时候往往会设置小于 1 的温度系数.

7. 大模型幻觉

就是大模型会胡说八道, 输出一些不符合事实的内容. 本质上因为 Causal Transformer 是一个概率模型, 所以在 next token prediction 的时候是根据只是根据计算结果选择了概率大的 Token 输出. 解决方法有, 比如修改训练数据, 让大模型性能够说不, 这种方式的依据是大模型参数那么多, 应该有些参数是和模型自身的困惑度之类相关的, 所以只要训练这些参数, 让模型能在在这个激活值比较大时回答不即可. 还有就是增加模型的上下文, 比如 RAG, 对推理问题还有 CoT 等等.

8. repetition_penalty

将已生成词的概率除以 repetition_penalty. 大于1: 减少重复词概率; 小于1: 增加重复词概率. 现在一般都设成 1 了, 即不考虑这个东西了.

9. 长文本问题: 与推理结果相关的内容在文本中的位置会怎样影响模型的推理结果?

尾>首>中>随机. 因为整体而言, 模型的 attention 会集中分布在头部和尾部, 中间的 attention 会少.

10. 什么是压缩即智能?

一种理解是模型在训练集上的 perplexity, 越小说明模型对数据记忆地越好, 也就是模型把数据集很好地压缩到了模型中. 而 perplexity 其实就是训练的 loss, 所以就是 loss 越低, 模型的泛化性越好, 完成各种人类任务的能力越好.

11. 内存不够时, batch_size 和 lr 的调节关系.

lr 与 batch_size 同向变化, 但倍数为 batch_size 变化的根号.

12. LLM 在数学问题上为什么 majority voting 总是有效?

因为 LLM 是一个概率模型, 假设 LLM 做对某道题的概率是 p, 如果只 sample 一次, 那就是 p, 但是如果 sample 多次, 那么正确答案出现次数大于一半的概率就可用一个二项分布来算, 而当 p > 0.5 的时候, 这个结果都是严格大于 p 的. 反过来, 如果 p < 0.5 那投票也不会有效.

13. Adam 和 AdamW 的区别?

Adam 的 weight decay 是应用在梯度上的, 因此会参与一阶和二阶矩的计算; AdamW 将其移除, 直接放在最后更新上. 即: 对 Adam $g = \delta f/\delta w + w$, 而对 AdamW: $w = w - lr(动量+w)$ (此处省略了 weight decay参数)

14. 二分类如何处理多分类?

两种策略: ovo, 训练 n(n-1) / 2 个二分类器; ovr 训练 n 个二分类器. 相应地, 混淆矩阵也有 n(n-1) - 2 或 n 个. F1-score 也有两种计算方法: 对每个分类器的 P 和 R 求平均, 再算 F1; 对每个分类器的 TP、TN、FP、FN 求平均, 再求 P R F1.

15. k-means 的过程

选择 k 个初始聚类中心, 每个样本计算到 k 个中心的距离, 选择最小的一个加入那个聚类中, 每个聚类重新计算聚类中心. 重复直至收敛.

16. LSTM

忘记门、输入门、输出门. 两个 memory $C _{t-1}$ 和 $H _{t-1}$.

17. GRU

更新门 (加入)、重置门 (忘记).

18. attention 和 LSTM 的 GATE的不同

首先两者有些相同点, 都是用加权的方式控制过去信息对当前信息的影响, 使得当前的输出依赖于历史. 但是 LSTM或者GRU 的 GATE 是自回归, 所以它后一个时刻如果想对之前某个时刻的信息进行增强是没有办法的, 因为它自回归的特性决定了前面的信息到后面只会越来越少, 所以不可避免的会有长时遗忘的问题. Attention 则

19. 分组卷积 和 普通卷积的区别

分组卷积分组融合, 所以如果组的个数等于通道个数那就是不融合.

20. xgboost

叶子的值作为参数, 叶子的个数可作为模型的复杂度. 核心理念为为多个模型 (多棵树) 去进行函数拟合, 后一棵树拟合前一棵树的残差. 按顺序训练, 因此后一棵树训练的时候前一个树的参数以及复杂度均为常数 (树的复杂度除了叶子个数以外, 还会加入权重的 L2 正则, 因为 w 越大越容易过拟合. 即多个弱分类器要比一个强分类器泛化性好). 因为 xgboost 用二阶泰勒展开近似了损失函数, 所以对 xgboost 的每一棵树, 在划分一定时, 其最优权重是个解析解 (对二阶泰勒展开的) (即开口向上的二次函数), 因此没棵 Tree 优化的实际上是是否要增加开新分支增加新的叶子结点. GDBT 对权重的求解则用的梯度下降的方式.

21. 对比学习的温度和大模型推理时的温度有什么区别?

对比学习的温度是用来稳定训练的, 一般是设置为0-1, 好处在于, 当模型分类正确时, 因为小于 1 的温度会使得概率分布趋于 one-hot, 所以产生的梯度就会偏小, 对模型起着稳定的作用; 而当模型分类错误的时候, 也是因为概率分布会趋于 0-1, 所以此时正确类的概率会比没有温度的时候更小, 于是就能够产生更大的梯度, 从而加速模型的收敛.

一些数学上的东西

• 蒙特卡洛方法: 用估计值 (多数情况为均值) 近似理论值. 当采样次数够多, 估计值就会收敛到理论值, 如强化学习中对状态价值的估计、对 KL 散度的估计.
• 二项分布: n 次伯努利重复实验正例出现个数的分布.
• 泊松分布: 单位时间随机事件发生次数的分布, 如一个小时加油站进站车的个数. 当 n 很大时, 二项分布可用近似.
• B分布: 是定义在 (0, 1) 的概率分布. 有 $\alpha$ 和 $\beta$ 两个参数, 两者相等时概率密度关于 0.5 对称. 两者均为 1 则退化为均匀分布.

位置编码

因为自注意力不感知位置信息, 所以需要位置编码来辅助其学习文本的语序 (但其实因果注意力是能够感知位置的.). 当下的大模型基本用的都是 RoPE.

1. 绝对位置编码: 编码 Token 的绝对位置.
   • 正弦位置编码 (Sinusoidal): "Attention is all you need" 原文所采用的.
   • 可学习位置编码: GPT2 采用的. 与正弦位置编码一样直接和输入 Token 相加.
2. 相对位置编码: 编码 q 和 k 的相对位置.
   • 旋转位置编码 (RoPE): 用向量的角度来代表位置, 因而施加的方式是与投影后的 q, k 相乘.
   • ALiBi: 直接加在注意力矩阵上, (-n, ..., -1, 0) 表示相对当前 Token 的位置.

问答

1. 频率项的计算?

RoPE 和 Sinusosial 都有统一的频率 (角度) 计算方式:

# k / (base)^{2i/d}, 其中 k 是 Token 的位置, i 是 Embedding 的位置, d 对 正弦位置编码是 Token 维度, 但对 RoPE 是 Head 的维度
base, seq_len, n_embd = 10000, 1024, 768
t = torch.arange(seq_len)
freqs = 1.0 / (base**(torch.arange(0, n_embd, 2)/n_embd))
# (seq_len, n_embd//2)
freqs = torch.outer(t, freqs)

2. RoPE 是如何处理训练长度以外的长度的? 即 RoPE 如何进行长度外推?

有两种可以结合的方式. 第一种是对 RoPE 的旋转弧度进行放缩. 最开始是根据新的序列长度和预训练长度的比值去缩小旋转弧度. 后来有文章指出, 因为 RoPE 对于位置越靠前的 embedding 旋转角度越大, 频率越高, 所以越靠前的特征对位置信息的训练越足, 外推能力越强, 因为见到的角度变化越多, 而越靠后的受到的训练越少, 外推能力越弱, 所以对不同的特征进行相同程度的放缩会导致高频信息的丢失. 因此后续的方法有像 ntk-aware 的在进行长推理的时候把 base 扩大; 也有像 ntk-by-parts 的对靠前的特征的角度不做放缩, 只对靠后的进行放缩. 现在用得更多的应该是 dynamic ntk, 就是对推理长度等于训练长度的部分不进行操作, 当推理长度大于训练长度时, 动态地根据当前的长度放大 base. 第二种是对注意力分数进行放缩, 因为 RoPE 在 qk 相乘的时候转换为相对位置信息的, 所以在缩小了旋转角度之后, qk 之间的旋转弧度就变小了, 两者内积得到的注意力分数也相应的增大了, 最终会导致注意力分数分布的变化. 所以就要对注意力分数进行放缩, 方式可以是像 YaRN 用一个用推理长度和训练长度计算出来的问题系数放缩, 也可以是 LogN-Scaling. 此外 RoPE 的远程衰变性对最远的 Token 也不是直接衰变到 0 的, 而是会振荡, 这使得模型在长窗口也能够召回一些相关的 Token.

$$
(\frac{l'}{l})^{d/(d-2)}
$$

3. RoPE 的远程衰减特性是什么?

远程衰减性是指 qv 的内积随着它们相对距离的增加会有衰减的趋势, 这就给模型加入了越远的 Token 与当前 Token 越不相关的先验. (theta 要随着位置单调递增才行, sinusosial 就可满足). (本质上是旋转角度的余弦 $\cos n _{relative}\theta$ 在 $(0, 1)$ 单调递减, 因此实际上远程衰变性是由低频的、旋转角度小的、位于后方的特征保持的. 高频的、旋转角度大的因为转动较快, 所以呈现出的是周期性, 而低频的才呈现出单调性, 因此远程衰减性是由低频部分维持的.)

4. LogN-Scaling and YaRN 中 缩放公式的区别.

LogN:
$$
\text{softmax}(\frac{\mathcal{\kappa\log n}}{d}QK^T)V
$$

其中 $\kappa$ 是超参数, $n$ 是新的序列长度, $d$ 是注意力头的维度, 若要使得对预训练长度内的性能不变, 则 $\kappa$ 可设为 $\sqrt{d}/\log n _{pre}$, 最终得到:
$$
\text{softmax}(\frac{\mathcal{\log _{n^{pre}} n}}{\sqrt{d}}QK^T)V
$$

YaRN:
$$
\text{softmax}(\frac{1}{t\sqrt{d}}QK^T)V
$$

其中:

$$
\sqrt{\frac{1}{t}}=0.1*\ln(\frac{n}{n^{pre}}) + 1
$$

LogN 的推导原理: 熵不变性, 即新长度下和旧长度下, 同一个 Token 注意到的 Token 不会发生变化. 见苏剑林文章.

5. 还有其他的外推方式吗?

Window Attention, 就是把注意力往前看的对象限制在一个窗口内, 低层用较短的窗口, 高层用更长的窗口. Qwen 用的是 dynamic ntk, logN-Scaling, 和 window attention.

6. Causal Attention 不具有置换不变性, 为什么现在的 Decoder-only 架构还需要位置编码?

置换不变性指 Token 的次序不影响输出结果, 双向注意力是具有置换不变性的, 但单向注意力没有. 有研究指出, 单向注意力不需要位置编码, 即 NoPE 也能取得很好的效果, 一种解释是单向注意力因为不同位置的 Token 注意力加权求和的元素个数不同, 即第一个位置只和其自身, 第二个位置是前一个位置和自身... 所以输出结果的方差也不同 (假设输入都是同分布的情况下), 而位置信息就编码在这些方差中. 但是 NoPE 实现的是绝对位置编码, 而实验上的结果显示相对位置编码更适合自然语言, 并且 NoPE 也没有 RoPE 等带来的远程衰减的先验, 即对距离越远的信息应该给予给少的关注, 所以目前来说加上相对位置编码还是更好的.

Transformer

问答

1. 为什么 q, k 转置相乘后还要除 $\sqrt{d}$ ($d$ 为注意力头的维度) 再做 softmax?

这和模型的初始化以及标准化想要解决的问题是类似的. 为了神经网络的训练稳定, 防止梯度爆炸和消失, 我们会希望输入和输出的某些统计特性是一致的, 比如都是均值为 0, 方差为 1, 或者二阶矩都是 1. (括号内的不说. 基于此, Xavier 将 Linear Weight 初始化为均值为 0, 方差为 1/m (因为输出的方差是mVar(输入), m 是输入维度, 也好理解 m 个相加嘛); kaiming初始化针对 relu 会让一半的数值归零, 将带有 relu 的网络的初始化方差调整为 2/m. 更直接的方法是标准化 (LayerNorm, BatchNorm...), 即强行让输出为正太分布, 或者直接将输出除以 1/$\sqrt{\text{m}}$.) 假设 q, k 都服从标准正太分布, 那么其内积的方差 (二阶矩也是) 就是 $d$, 这会导致注意力分数的极差很大$(-3\sqrt{d},3\sqrt{d})$, 那么 softmax 之后权重最大的就会接近 1, 最小的接近 0, 整体趋于一个 one-hot 的分布, 所以会带来较严重的梯度消失问题. 解决办法就是除 $\sqrt{d}$, 让 qk 内积的方差变回 1, 或者初始化 qk 的线性层时让方差多除个 $\sqrt{d}$, 让 qk 输出的方差变成 1/$\sqrt{d}$, 这样最后内积的方差就也还是 1 了.

2. 为什么现在多数模型用 PreNorm 而不是 PostNorm (原版 Transformer 和 BERT 采用)? 两者各有什么特点?

PostNorm 是对残差连接后的结果进行标准化, 带来的结果是前面层的通过恒等分支传递来的残差的效果随着层数的推进, 因为 Norm 而被削弱了; PreNorm 则恰恰相反, 它是对残差连接前的结果进行标准化的, 所以每一层的残差都会平等地传播到最后. 这带来的效果是, 因为残差是为了更好地训练, 所以 PreNorm 的模型更好训练. 但实际上有的文章指出, 在预训练效果一致的情况下, PostNorm 微调的效果会更好. 因为 PreNorm 对过往的残差都是等权相加的, 所以当层数很深的时候, 最深几层的输出结果会很相似, 体现在梯度上就是 PreNorm 模型低层的梯度会比高层的梯度大, 最终呈现的效果就是 PreNorm 有效深度降低. 而 PostNorm 则因为对前面层的残差会进行削弱, 所以虽然训练更难了, 但最终对高层的训练也会更加充足.

3. 为什么在最后的投影层前要对输出进行标准化?

因为现在多数大模型都采用的是 PreNorm 的架构, 即只标准化残差分支, 而不标准化恒等分支, 所以最后传递到投影层的结果是很多个残差相加的结果, 这就导致输出的方差比较大, 所以要通过标准化缩小方差.

4. 为什么现在都是 Decoder-only 架构?

Decoder-only 用的是 Causual-Attention, 即 Token 只对前面的位置求注意力. 相比于双向的注意力, 其好处在于生成的注意力矩阵是满秩的, 因为注意力矩阵是由 qk 内积得到的, 而 qk 其每个 head 的维度是远小于序列长度的, 所以双向注意力生成的是一个低秩的矩阵, 而单向注意力因为是上三角或下三角的, 而 softmax 又保证元素非 0, 所以其行列式非零, 进而是满秩的, 满秩矩阵的表达能力要强于低秩矩阵, 所以理论上来说 Causual-Attention 的表达能力更强.

Pytorch

问答

1. model.eval(), with torch.no_grad() 的不同

   • model.eval() 只用于将 dropout 和 batchnorm 设置为推理模式 (即让所有单元激活, 用学习到的全局 mean 和 var 计算 batchnorm), 其他行为与 model.train() 一模一样 (仍可梯度回传).
   • with torch.no_grad(): 创造一个空间, 将生成的中间变量的 requires_grad 设置为 False (不改变已有参数的梯度情况), 因此不再会保留计算图, 这些中间变量在后续阶段的 requires_grad 仍是 False , 一般用在推理或不需要梯度的中间变量计算.

资源、硬件、分布式相关

问答

1. FlashAttention 的原理?

核心目的是减少 GPU 高速的 SRAM 和 较为慢的 HBM 间通信的次数, 因为当前 GPU 的计算能力是大于通信能力的, 所以 IO 是瓶颈. 具体做法是: 原本的 softmax, 我们需要先找到注意力分数中的最大项, 然后把所有的注意力分数都减去这项, 防止算指数的时候溢出, 这需要一轮的 IO, 然后计算 softmax 的分母要一轮 IO, 最后得到注意力权重然后和 value 相乘要一轮 IO, 共 3 轮. Flash Attention 的做法是, 把求最大注意力分数、计算 softmax 分母、以及注意力权重和 value 相乘都转换为一个递归的等比数列的形式, 以此实现在一轮 IO 中完成所有的计算.

2. 如何根据模型的参数量估计推理和全量训练的显存?

模型占用的显存有 3 个考量: 1) 模型自身占用的空间. 这取决于模型的精度以及参数量, 每 B 字节的参数一般对应 1G 的内存, 因此 FP16 的 7B 模型占用 14 G. 2) 优化器状态参数占用的空间. 对于 AdamW, 因为要为每个参数同时维护一阶和二阶动量, 所以占用空间是模型参数的 2 倍; 对于带一阶动量的 SGD, 占用空间为模型参数 1 倍; 对于不带动量的 SGD, 则不占用内存. 3) 动态的显存开销. 包括 a). 模型自身的梯度. 因为和模型精度相同, 所以占用内存与模型相同; b) 优化器的中间状态. 一般也和模型精度相同; c) 前向传播激活值. 通用公式为 $$(4.6894\times 10^{-4}\times N+1.8494\times 10^6)\times B\times L \times precision$$ 其中, $N$ 为参数量, 梯度和优化器中间状态一般在反向传播出现, 激活值一般在前向传播出现. 因此, 推理时只需要考虑 模型以及激活值, 而训练时则需考虑 模型、优化器以及max(梯度+中间状态, 激活值). 若只考虑 fp16, 则粗略地估计为: 推理显存约为 23N G, 训练约为 810N G (混合精度则还要加，大概16 N). 此外还要考虑框架开销和显存碎片, 因此要多预留 30% 左右.

Fig. 1. Memory Usage

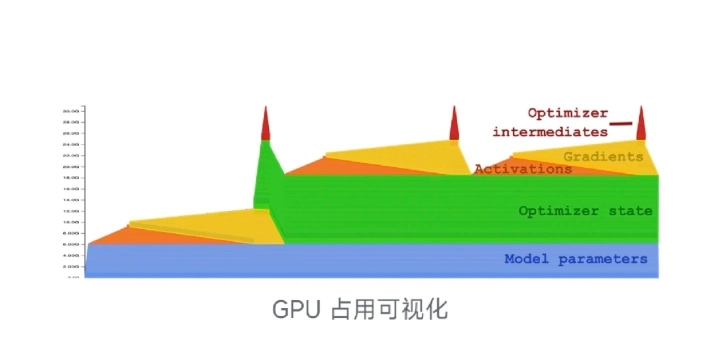
3. 混合精度 (fp32/bf16) 训练时, 参数、梯度和优化器状态的精度各是怎么样的?

混合精度训练时, 显存的节省与参数、梯度和优化器无关, 仅来源于激活值. 因为: fp32 训练时, 参数+梯度+优化器=4+4+4*2=16; fp32/bf16 时, 参数+梯度+优化器=2+2+4+4*2=16, 其中额外的 4 来自原始 fp32 参数的备份. 因此除激活值以外的开销是不变的.

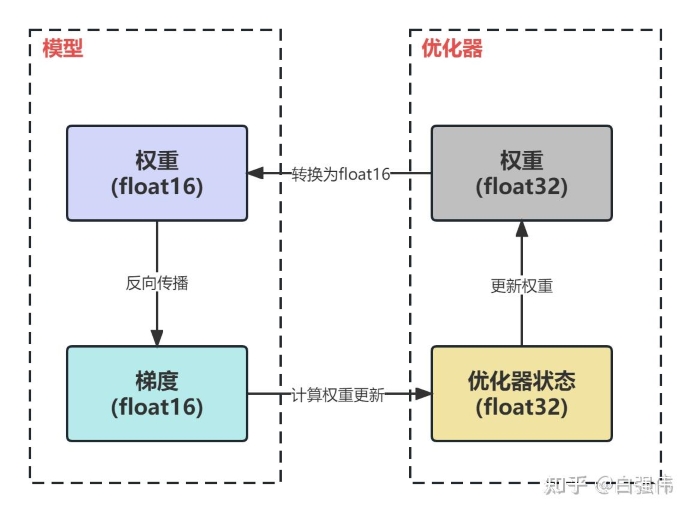
4. 混合精度训练时, 前向、反向传播以及优化器的精度变化各是怎样的?

前向传播时, 输入、权重以及输出的精度都是 bf16, 部分归一化和累加计算 (e.g., softmax) 为了防止溢出会用 fp32; 反向传播时, 梯度的计算用的是 bf16, 梯度的累加用的是 fp32, 防止溢出; 优化器更新时, 梯度转为 fp32, 更新 fp32 的权重副本、优化器状态, 然后 fp32 权重转为 fp16 进行下一轮的前向、反向.

Fig. 2. Mixed Precision Training

1. 介绍一下模型并行 (MP) 和 数据并行 (DP).

模型并行是在不同的 GPU 中对相同的数据做部分模型的计算, 现在用的更多的是 megatron 的张量并行, 即把一个模型的线性层、attention head 分块放在不同的 GPU 中; 数据并行是在不同的 GPU 中对不同的数据做全模型的计算, 最简单的有 DDP, 每张卡都装相同的整个模型, 接受不同的输入, 还有 ZeRO 把优化器、梯度、参数都切分开, 放在不同的卡, 在需要用到的时候再通过 GPU 通信传输过来.

6. 介绍一下 megatron 以及分析一次前向/反向传播 megatron 的通信量.

megatron 是针对 Transformer 的模型并行策略 (但也可以拓展到其他架构). 假设有 k 张卡, 则基本的做法为: 对于 Embedding 层, 每张卡只存有 1/k 的 Token 的 Embedding, 因此对本卡查不到的直接返回零向量, 然后通过一次 allreduce(sum) 从其他卡中拿到没有的 Token 的 Embedding; 对 Attention 层, 每张卡只有 qkv 投影层的 1/k 列, 等价于每张卡各处理不同的头, 然后每张卡只有 o 的 1/k 行, 最后还是通过一次 allreduce(sum) 得到最终的输出; 对 FFN 层, 每张卡只有上投影层的 1/k 列, 下投影层的 1/k 行, 最后还是通过一次 allreduce(sum) 得到最终的输出; 对最后的投影层 (n_embd x vocab_size), 每张卡只有 1/k 列 (无论是否与 Embedding 层共享参数), 此时因为 vocab_size 很大, 因而通讯量巨大, 故会将其与 softmax 一起处理, 即本卡计算 softmax 的分母, 然后只 allreduce(sum)分母, 这样对一个batch和一个token通信量就只是一个标量. 前向传播时, 每个 Layer 两次通信, 此外头尾各一次, 因此通信个数为 $2\cdot(n _{layers}+1)$, 通信量为 $2\cdot(n _{layers}+1)\cdot b\cdot l\cdot d$. 反向传播通信开销与前向传播一致 (因为对每一层, 输入 x 是 repeat 的, 所以反传时要在此处 allreduce).

• allreduce: reduce (求和、求平均) + broadcast (广播到所有设备).

7. 介绍一下 ZeRO.

zero1: 分割优化状态参数. zero2: zero1的基础上还分割梯度. zero3: zero2的基础上还分割参数. 每张卡接受不同的 minibatch, 前向传播时, allreduce 参数, 反向传播时, allreduce 参数、梯度和优化器状态.

8. 有用过 DeepSpeed 吗, 介绍一下?

用过 accelerate + deepspeed. 基于 ZeRO 的 DP 框架.

9. 流水线并行 (PP)、序列并行 (SP) 和 专家并行 (EP) 各是什么?

PP: 按 Layer 切; EP: 不同专家放不同 GPU; SP: Sequence 维度的数据并行, 即把序列的分块放在不同的 GPU.

10. NCCL (NVIDIA Collective Communications Library) 的通信方式:

NVLinK (GPU 直连) > P2P (GPU 通过 PCI-E 直连) > PCI-E + CPU RAM (GPU1 -> CPU -> 内存 (通过 PCI-E) -> CPU -> GPU2)

以下通信量分析均把收发视作一次通信.

11. 分析 Pytorch 中 DP 和 DDP 的通信量 (设 $N$ 为 GPU 个数, $\psi$ 为参数量)

DP 是单进程多线程的模式, 因而有一个主线程完成所有的收发工作. 主线程接收 $(N-1)\psi$ 的其他线程的梯度, 在本地更新参数后, 将 $(N-1)\psi$ 的参数发给其他线程, 其他线程各只用收发 $\psi$ 的参数. DP 的负载是极度不均衡的, 已被弃用. DDP 是多进程的模型, 进程间使用 Ring-AllReduce 的技术进行通信, 即进程间环状地向相邻进程传输不同的数据 (e.g., GPU0 -a-> GPU1 -b-> GPU2 -c-> GPU3), 这样经过 $(N-1)$ 轮, 每个 GPU 上都有 $\psi/N$ 的参数是通信好的, 该阶段称 Scatter-Reduce; 然后通过 AllGather 阶段, 同样地环状传递通信好的参数, 经过 $(N-1)$轮, 所有参数同步完毕, 总的通信量近似为 $2\psi$. 需要注意, DDP 只通信梯度, 而梯度后传是串行的, 所以已经计算好的梯度的参数积累到一定程度后就会进行通信.

12. 分析各个 ZeRO 的通信量

zero1: 前向传播时无需通信, 反向传播时, 每个 GPU 向拥有那部分优化器的 GPU 发送梯度, 该 GPU 同时接收其他两个 GPU 传来的梯度, 通信量为 $(N-1)\psi/N$, 此外, 梯度更新后的参数要广播给其他 GPU 也要接收其他 GPU 广播给自己的参数, 通信量 $(N-1)\psi/N$, 总通信量 $2\psi$, 与 DDP 一致; zero2: 通信量亦为 $2\psi$, 因为没有优化器本来也没必要存储梯度了; zero3: 前向传播要参数广播, 通信量 $(N-1)\psi/N$, 反向传播计算梯度要参数广播, 通信量 $(N-1)\psi/N$, 梯度要广播, $(N-1)\psi/N$, 因为参数只在本地, 所以此时更新参数无需再广播, 故总的通信量为 $3\psi$. 可见, zero1 和 zero2 均不增加通信量, 所以一般用到 zero2. 但如果显存吃紧, 可用上 zero3.

13. vllm 原理

PageAttention + shared kv cache (有同样上文的共享 kv cache) 加速推理.

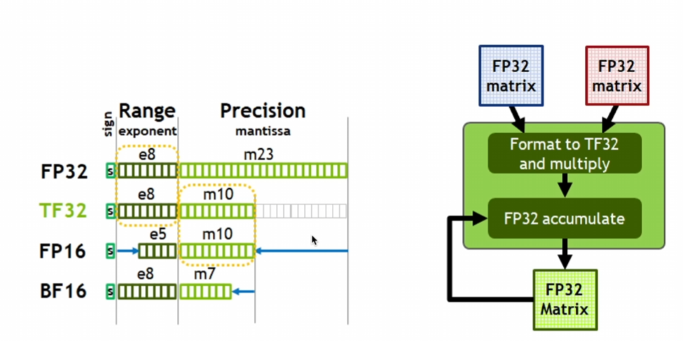
14. 为什么 bf16 更受欢迎?

一方面是 bf16 相比于 fp32 只裁剪了精度, 指数位都是 8 位, 而 fp16 的指数位是 5 位, 因此 bf16 和 fp32 的数值范围是一致的, 能够较好的保持反传梯度的稳定性, 不太需要 loss scaling; 然后就是 bf16 的效率要稍微高一点, 同样是因为它保持了和 fp32 一样的指数位, 所以转化的时候只要最后补零就好了.

Fig. 3. Nvidia BF16

各类大模型架构

GPT

传统派. GPT2 是 可学习的绝对位置编码、Pre-layernorm、gelu、最后的解码层和 Embedding 共享参数, 以及除了最后的解码层, 其他的 Linear 都有 bias. 后续的版本应该都用上了 RoPE、silu 等.

Qwen

不同点:

1. 注意力层
   • 只有注意力层的 q_proj、k_proj、v_proj 有 bias, 说是注意力层的 bias 能增强模型外推能力.
   • GQA 代替 MHA, 减少 k, v 注意力头的个数, 相当于降低 k, v 的维度, 进而减少 kv-cache 需要的内存. 最后求注意力还是要通过 repeat 让 kv 头的个数和 q 对齐.
2. 前馈层
   • 激活函数用的 silu.
   • 用的 gated-mlp, 即有三个 Linear 层, 相应地为了保持参数一致将隐藏层的扩大系数降低为 8/3.
3. 位置编码
   • 用的 RoPE, 施加在 q_proj、k_proj 后的 qk 上.
   • theta=1000000
4. 其他
   • 最后的解码层和 Embedding 不再共享参数
   • LayerNorm 换为 RMSNorm, 降低计算量

问答

1. MHA, MQA, 和 GQA 的区别

MHA 的 qkv 头个数相等; MQA kv 只有一个头, 等价于所有头共享一组 kv; GQA 是 MHA 和 MQA 的折中, 即 q 的头是 kv 头的倍数, 等价于多个头共享一组 kv. MHA 能力最强, 开销最大; MQA 能力最弱, 开销最小; GQA 居中.

2. 实现 RMSNorm

class RMSNorm(nn.Module):

    def __init __(self, dim, eps=1e-6):
        super().__init__()
        self.dim = dim  # token 维度
        self.eps = eps  # 防除0
        self.w = nn.Parameter(torch.ones(dim))
    
    def forward(self, x):
        rms = torch.rsqrt(torch.mean(x.pow(2), dim=-1, keepdim=True) + self.eps)  # 等价于除以均方根的倒数
        return x * rms * self.w

3. 为什么用 RMSNorm?

RMSNorm 去掉了过去标准化方法都有的去中心化操作, 就是 RMSNorm 只是除以了所有特征的均方根. 原文的实验表明模型 RMSNorm 和 LayerNorm 的表现差不多, 但是 RMSNorm 因为要的计算更少所以效率更高.

4. 对比各种激活函数 relu, gelu, silu, 为什么现在的模型多用 silu?

relu=max(0, x), 能够有效地为模型提供非线性性, 但对负输入永远为 0, 可能导致一些神经元在训练过程中一直不更新; gelu=x*f(x), 其中 f(x) 标准正态分布的累积分布函数 (即小于x的比例), gelu的输出接近正态分布, 和神经网络的权重分布较为一致, 且正负值的过渡更为平滑, 但是计算较复杂; silu=x*sigmoid(x)=x/(e^(-x)+1), 与 gelu 一样的平滑作用, 计算比 gelu 简单. 实验结果显示 silu 更好.

LLAMA

和 Qwen 的架构差不多 (或者说 Qwen 和 LLAMA 的架构差不多)

DeepSeek

MLA 优化的点主要在 kv cache, 因为目前推理阶段的瓶颈是 IO, 所以单卡/单机能缓存更多的 kv 就能显著地提升推理的速度. 至于训练部分, MLA 并不会变快, 因为实际上计算量还上去了.

问答

MLLMs

多模态模型, 当前一般指图片+文本的模型. 通常由两大模块组成: LLMs: 通常为用 Instruction SFT 后的大语言模型而不是 PLM; Vision encoder: CLIP、ViT 等. 一般冻住. 常见的融合方式有两种:

Fig. 4. VLM

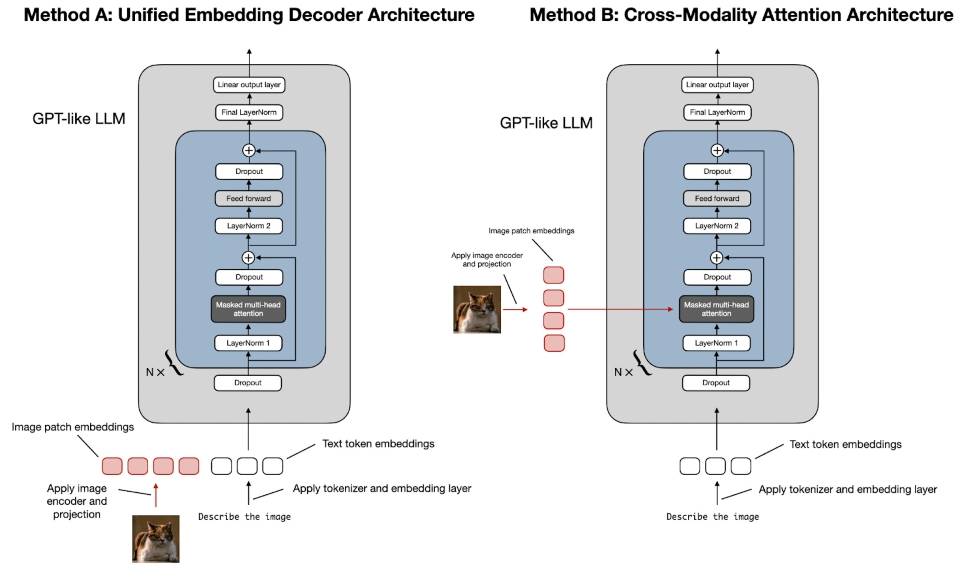
1. Decoder-only: 仅在序列维度将编码、投影后的 Image Patch 与文本拼接. 优势为不需要改变 LLMs 的结构, 且在 OCR 相关的问题上有较高的精度. 劣势为计算复杂度过高, 因为拼接后序列长度的增长将导致复杂度平方级地增长. 模型有 LLaVA (MLP将视觉投影到文本)、Qwen-VL (类似Flamingo的 perceiver resampler 作为桥梁). 典型的训练流程为:
   • Pretrain: LLM 被冻住, 只训练投影模块 (如 MLP), 有些模型也会同时训练 Vision encoder;
   • SFT: 投影模块与 LLM 同时训练, 有些也会训练 Vision encoder.
2. Cross-attention-based: 在原始的 LLM 的 Decoder 中额外增加 Cross-attention 模块 (每层或者每隔 k 层), 将 Text 作为 q, 编码、投影后的 Image Patch 作为 kv. 优势为计算效率高. 代表有 Flamingo、LLAMA 3.2-V. 典型的训练流程为:
   • Pretrain & SFT: 一般都只训练投影模块 (Flamingo 的叫 perceiver resampler, NVLM 觉得这会搅浑空间信息, 所以将其简单地替换为一层 Linear, 用以对齐 Image Token 和 Text Token 的维度) 和 Cross-attention 模块. 此外, Cross-attention 模块也可视图片的有无进行激活, 因而其对 LLM 原本的文本处理能力是无损的 (当然也不会带来提升).

NVIDIA 有个混合两种方式的模型 (Hybrid), 效果比 Cross 的好, 比 Decoder 的差, 效率也介于两者之间.

Fig. 5. NVLM

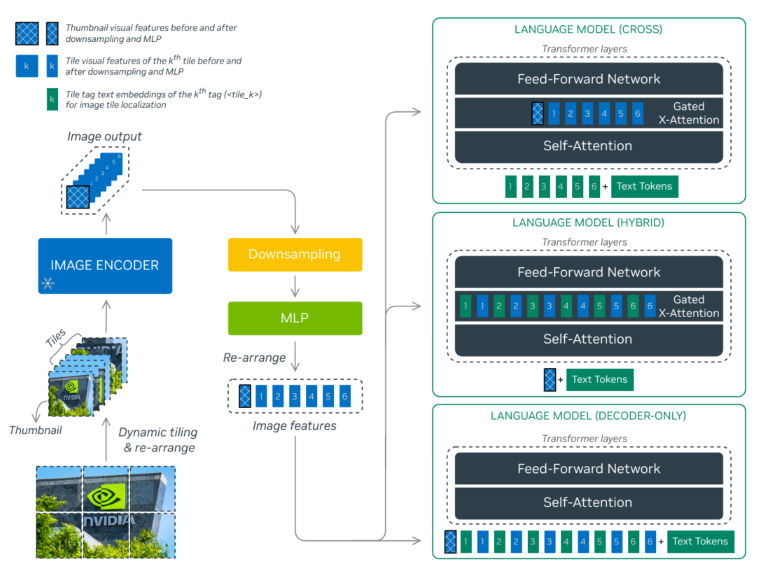
问答

1. 目前的多模态模型中, 视觉和文本结合的方式是怎样的?

见上.

2. 低分辨率训练的 Vision encoder 如何处理高分辨率的图片?

把高分辨率的图片用低分辨率的比例切分为多个 tiles, 如对 896x672 的图片, 对用 224x224 训练的 Vision encoder, 会先把高分辨率图片切分为 (896/224 x 672/224) 共 12 个 tiles, 然后分别送进 encoder, 最后得到的 tokens 拼接起来. 比如若 patch size 为 14x14, 那么每个 tile 就有 256 个 tokens, 12 个就总共有 3072 个 tokens. 同时加入一个 token 切分每个 tile (NVLM 的做法).

3. 如何解决 VLM 训练后模型的纯文本处理能力下降的问题?

使用 Cross-attention 的架构而不是 Decoder-only 的架构; 在 SFT 阶段加入高质量的纯文本数据.

4. BLIP & BLIP2

BLIP 类的模型是想用一个模型来同时完成图文匹配和根据图片的文本生成任务. 因此, 除了图片编码器以外, BLIP 还三个并行的 Attention 架构的文本编码或解码器. 其中一个解码器负责的是和 CLIP 一样的任务, 即通过图文对比学习来更新, 另一个解码器是带 cross-attention 的, 其中cross attention 用于输入图像信息, 负责的是图文匹配任务, 即完成一个二分类的任务, 最后一个解码器是带 cross-attention 的 因果子注意力架构, 完成根据图片的文本生成任务. 三个 attention 大部分参数都是共享的, 除了 causual self-attention 是单独的之外. BLIP2 论文中对标的主要是 FLAMINGO 架构, 他认为 FLAMINGO 用来对齐图文的 perceiver resampler 太弱了, 所以是先用和 BLIP1 一样的任务对用BERT初始化的 Image Transformer 和 Text Transformer 进行第一阶段的训练, 其中 Image Transformer 加入了 cross-attention 层, 以及可学习的 Query Token, 来压缩图片信息, 最后图文生成的时候是只用 Image Transformer 生成 可学习的 Token 在和 Image 交互后的编码, 投影, 然后直接和文本拼接在一起输入冻结的 LLM中.

Fig. 6. BLIP2

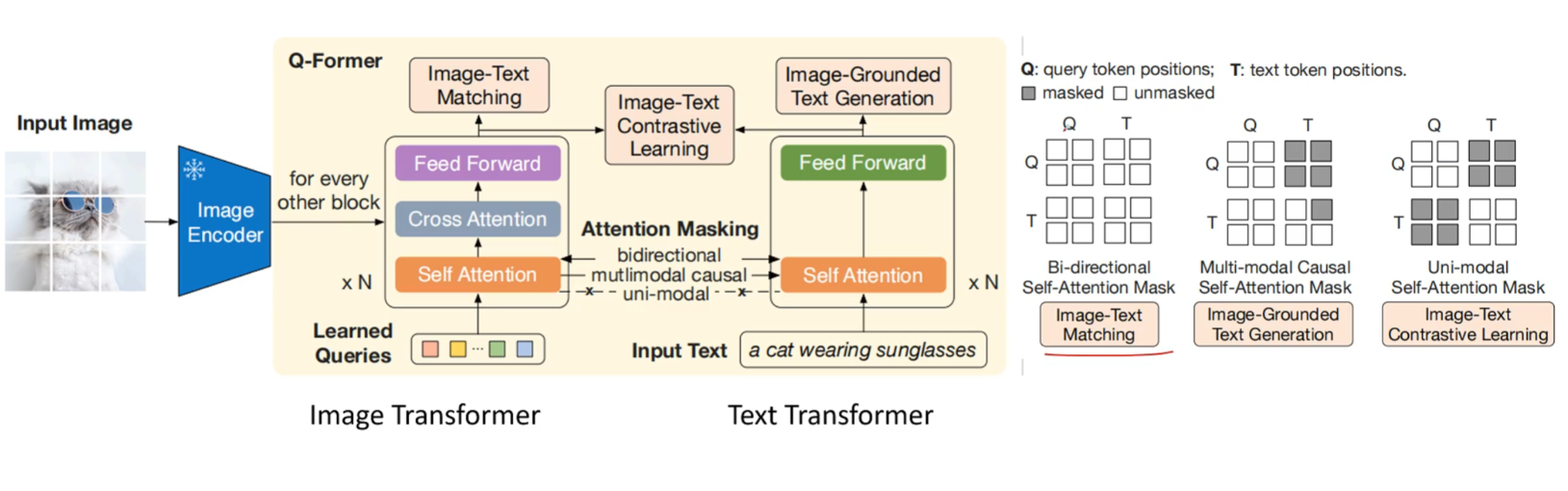
Pre-training

问答

0. 什么是 BPE, 为什么要 BPE?

Byte-Pair Encoding. 就是不断地把一起出现次数多的词 merge 到一起加入词汇表中的算法. 一方面是人类是不断地在创造新词的, 我们不能每创建一个词就把 Token 加一, 因此要把单词拆分, 因为词汇的创造往往是基于已有词汇的; 另一方面字母 Level 的拆分没什么意义, 所以需要 BPE.

1. 为什么自回归是最主流的预训练方法? 此外还有什么预训练方法?

和下游任务契合度高, 只需要调整 Prompt 就可以处理各种任务, 而像 Bert 这类的掩码填空则还要多加一个投影头. 还有像 Bert 这种双向注意力模型的掩码后填空的预训练方式 (MLM). BERT: 掩码的方式是 80% 掩, 10% 替换为别的 Token, 10% 啥也不干. 还有一个任务是 Next Sentence Prediction, 给两个句子, 判断两者是否相邻. BERT 的三个 Embedding (Token, Position, Sentence, 都是 Learnable 的). BERT 处理多任务: 分类-用头的[CLS]+额外的投影头, "海底捞针": 额外的 [S] 和 [E] 分别表示句子的开始和结尾, 每个 Token 和 [S]、[E] 做点积, 然后分别 SOFTMAX.

2. 增量预训练 (Continued Pretraining) 的方式和技巧

用和最初预训练时相同的学习率 warmup-decay 方式, 在新的数据集中加入少量 (5%, 10%) (当分布差异不是特别大的时候replay 5%原始数据，当分布差异特别大的时候10%-20%原始数据) 的最初预训练数据, 避免遗忘.

3. 什么是推理计算 (test-time compute)? 常用的方法有哪些?

test-time compute 即通过让模型在推理时输出更多的 Token 来增强模型表现. 想法的来源是人在解决困难问题时往往会需要更多的思考时间, 对于语言模型来说也应当是成立的. 常用的方法让模型随机生成多个回答或者 Beam-search 生成多个回答, 然后 Best-of-N 选择最好的; 还有让模型自己对回答进行多次的修改. 通常简单的问题让模型自己修改即可, 而更困难的让模型生成多个回答会更有优势.

4. LLM 训练中数据质量的关键是什么?

多样性、涉及面广、去重复性、无风险性、正确以及结构化. 其中在结构化方面, json 格式的数据表现最好.

5. cosine 退火的周期要怎么选?

一般 warmup 后有多少步就退火多少步, 即最后一个 epoch 退火到 min_lr, 这样能在该步数下取得最小的loss. 也有研究表明退火阶段loss降得很快, 所以可以在 warmup 之后以最大学习率训练, 让 loss 缓慢下降, 等到要结束的时候再用约 10% 的最大学习率训练步数退火即可 (MiniCPM 的方法), 这样的好处是可以一直训练, 不像原始的 cosine 退火到 min_lr 即便再接着训练 loss 也变化不大.

6. LongContext 训练时, 短文本能力损失?

1. RoPE base 变化的影响, 进而导致 attention score 的变化, 具体就是远程衰变变慢, 模型对远近的感知变弱. 补救: 长短混合训练, 最好的短文本是 数学、代码, 因为其短程依赖性强.

7. Chinchilla scaling law 和 kaplan 的区别?

scaling law 是指在限定计算资源的情况下, 达到最低 train_loss 时模型参数和训练 token 的配比. chichilla 认为参数x2, token也x2, 而 kaplan 则认为是参数主导. 结论是: 训练的 Token 个数大约是模型参数的 20 倍时, 能到达最低的 Loss. (C=6ND (前向2, 反向4, 因为 1. 计算梯度更新本层参数 2. 计算输入梯度传导到前一层))

8. 数据集的构建方法

URL (过滤有害网站) -> 文本提取 (从 HTML 中提取纯文本) -> 语言过滤 -> 去重 (LocalMinHash) -> C4 filter (删掉 cookie 声明、太短的等等)-> 自定义的filter -> 删除个人信息.

Supervised Fine-tuning

问答

1. 有哪些高效微调的方法? 和全量微调比, 两者各有什么特点?

Fig. 7. PEFT

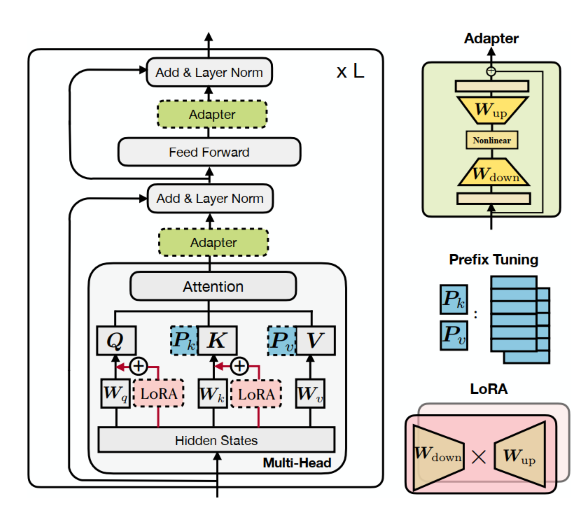
常见的高效微调的方法有像 Adapter, 在每层的残差连接前的 self-attention 和 ffn 后添加一个小的低秩参数矩阵; 也有像 prefix tuning 在投影后的 kv 前拼接几个可学习的 Token, prompt tuning 和 prefix tuning 类似, 只不过它不在每一层都添加 Token, 而是直接在Embedding 层后就把 可学习的 Token 拼接上去; LoRA 则是通过设置一个和线性层并行的低秩参数矩阵, 通过只微调这部分的参数达到轻量化微调的目的. 这几种方式都可以统一为通过特定的方式修改 Token 的hidden state, 即让模型的输出由 h 变为 h + $\Delta$ h, 原理上来说就是让模型的参数在一个较小的偏移空间内调整, 从而实现微调参数的同时避免灾难性遗忘现象. 不过前两者都增加了微调后模型的参数量, 所以会增加推理开销, 而 LoRA 的旁路矩阵可以直接并入原始参数中, 所以不会带来额外的推理开销. 和全量微调相比: 全量微调在微调任务下的表现要更好, 但 LoRA 等高效微调方式有着更好的泛化性, 即其遗忘现象要更弱, 因而能更好地保持微调前的模型在非微调任务下的表现.

微调参数的比例较大时, 微调 FFN 比微调 qkv 效果更好. (LoRA 微调 Self-attention 时, 调 qk 或 qv 的都有.)

2. 谈谈你对 LoRA 的理解, 以及最新的关于 LoRA 的研究有哪些?

LoRA 是一种高效微调的方法, 它通过在模型的参数层, 即 Linear 层旁增加一个参数量小的、低秩的矩阵来实现轻量化的微调. 这个低秩矩阵由一个下投影矩阵 A 和上投影矩阵 B 相乘得到, 其中 A 随机初始化, B 初始化为全零矩阵, 使得在训练初期 LoRA 不会干预模型的表现, 让模型能够渐进式地学习新的知识, 提升训练的稳定性. LoRA 的轻量化主要体现在反向传播上, 因为有很小的参数是需要梯度的, 所以反向传播的计算量和优化器需要的显存都会远小于全量微调. 同时, 因为 LoRA 可微调的参数空间较小, 所以最终的效果可能不如全量微调, 但胜在轻量化和遗忘现象不明显.

有像 DoRA, DoRA 把全连接层的向量用模长和方向表示, 然后单独优化模长, 而方向则用 LoRA 来优化. 这一方法取得了比 LoRA 更接近全量微调的效果. 还有像 QLoRA, QLoRA 把预训练模型用 4 bit 量化, 然后在这个量化的模型上进行 LoRA, 从而进一步节省微调时的内存开销.

3. LoRA 和全量微调该怎么选择?

如果都是对所有模块都进行微调, LoRA 因为是一个低秩的近似, 可学习的参数会比全量微调少, 所以开销, 但效果上多数不如全量微调. 其中对于 Instruction Tuning 类的, LoRA 可以通过增大 rank 来接近全量微调的效果; 而对于 Continued Pretraining, LoRA 不如全量微调. 所以 Instruction Tuning 用 LoRA 更好, 因为它一方面开销少, 另一方面遗忘少, 而增量预训练则还是全量的比较好.

4. SFT packing 是什么?

把多个 sft 样本打包到一个样本内进行训练, 可以加快模型的训练速度, 因为如果不 pack 的话短的 sft 样本就会有很多 padding token, 这对计算资源是极大的浪费. 计算的时候可以加 mask 让每个样本只关注自己的, 也可以直接 causal attention, 效果差不多.

5. SFT 常见的加速方法

多轮合并 (将多轮对话的合并为一个样本); packing.

6. 多轮合并和 packing 会带来什么问题?

可能会导致短的回答没有得到充分训练. 因为计算loss的时候有求 mean 的操作, 所合并或者packing后, 短回答的梯度相当于被长回答给稀释掉了, 所以相应地模型短回答的能力就变弱了. 解决办法就是让每个 Token 的loss 都是等权的, 就是有点麻烦. (似乎在大数据集上影响不大)

7. SFT 能学新知识吗?

很少. SFT 更多是对齐. 大模型的很多能力都是在预训练的时候获得的. 且太多知识的注入会影响模型遵循指令的能力.

8. SFT 的效果取决于什么?

LIMA (less is more for alignment) 指出, SFT 不需要堆数据量, 更重要的是 Prompt 的多样性和回答的质量.

9. 如何提升 sft prompt 的多样性?

给不同的 prompt 打 tag, 然后通过 tag 对分布进行调整; 用模型最后一层的 embedding 对 prompt 进行表示, 相似度高的 prompt 删除; 对简单的 prompt 进行难度升级, 如正着问 反着问.

10. In-context Learning 和 SFT 的关系?

ICL 是特殊的 SFT. 有研究表明, 对于相同 instruct 的最后一个 token 的最后一层的 embedding, ICL 和 SFT 后模型的差不多.

11. 如何在 SFT 中做 RLHF?

对数据进行处理, 给高质量回答加标签; 引入 DPO Loss.

12. SFT 更难改变哪些数据的模式?

代码等结构化、确定性强的数据. 因为对这些数据, 模型的困惑度低, loss 低, 所以少样本的情况下很难扭转.

13. SFT 学习率设置

一般为退火后的.

14. SFT 后复读机的原因

本质上是新生成的 Token 没什么用, 注意力权重很低, 所以下一个 Token 的预测结果还是它, 一直重复. 原因有: 1. 预训练没做好. 模型规模不够、数据不够多样, 导致 sft 数据超出了模型能力本身, 模型为了记住这部分数据, 就会打乱原始的 attention 分布, 就导致模型整个就不行了. 2. sft 数据虽然不需要过多, 但太少也不行, 因为 pretrain 的时候都是把文本 packing 到一起的, 所以模型没怎么学会停止输出.

15. 如何利用 ICL 增强预训练?

ICL 告诉我们, 模型可以从相关的知识中学习到通用的模式, 因此, 在预训练过程中, 与其简单地将不相关的文本拼接在一起组成长文本, 不如将相互关联的文本拼接在一起. 当然, 这会需要重新组织数据格式.

16. 模型如何获得 ICL 的能力?

是在预训练中获得的. 模型在预训练时, 会潜在地将具有相似格式的上文编码到一个特殊的隐空间中.

17. Function call 是怎么训练的?

大模型在 Function call 中的作用是根据用户的输入选取合适的 Function 和提取 Function 的输入, 然后是由实际的程序来执行这个 Function, 最后将响应发回给模型, 再让模型继续输出. 所以训练 Function call 大模型和普通的 SFT 差不多, 主要是数据格式上的区别, system prompt 里面会有能使用工具的具体描述, 包括函数名、函数描述、参数名、参数描述等. 训练的时候的 Ground Truth 就是 User Prompt 中提取到的参数, 按指定的格式, 一般是 json 那样的, 放到指定的 box 里面. 然后一个 function 框, 里面是 function 执行结果, 模型再从中提取输出, 按指定的格式输出. 类似下面这样.

"""
<|im_start|>system
You are a helpful assistant with access to the following functions. Use them if required -
{
    "name": "generate_invoice",
    "description": "Generate an invoice with specified details",
    "parameters": {
        "type": "object",
        "properties": {
            "customer_name": {
                "type": "string",
                "description": "The name of the customer"
            },
            "items": {
                "type": "array",
                "items": {
                    "type": "object",
                    "properties": {
                        "name": {
                            "type": "string",
                            "description": "The name of the item"
                        },
                        "quantity": {
                            "type": "integer",
                            "description": "The quantity of the item"
                        },
                        "price": {
                            "type": "number",
                            "description": "The price of the item"
                        }
                    },
                    "required": [
                        "name",
                        "quantity",
                        "price"
                    ]
                }
            }
        },
        "required": [
            "customer_name",
            "items"
        ]
    }
}
<|im_end|>
<|im_start|>user
I need to generate an invoice for a customer named John Doe. He bought 2 apples for $1 each and 3 oranges for $2 each.<|im_end|>
<|im_start|>assistant
<functioncall> {"name": "generate_invoice", "arguments": '{"customer_name": "John Doe", "items": [{"name": "apple", "quantity": 2, "price": 1}, {"name": "orange", "quantity": 3, "price": 2}]}'} <|endoftext|><|im_end|>
<|im _start|>function
{"invoice_id": "INV12345", "customer_name": "John Doe", "items": [{"name": "apple", "quantity": 2, "price": 1, "total": 2}, {"name": "orange", "quantity": 3, "price": 2, "total": 6}], "total": 8, "status": "Generated"}<|im_end|>
<|im_start|>assistant
The invoice has been successfully generated. The invoice ID is INV12345. The total amount for 2 apples and 3 oranges is $8. <|endoftext|><|im_end|>
"""

18. QLoRA

对 Base 的参数 NF4 量化, 即按正态分布的累计概率为每个概率区间赋予一个 NF4 中的 15 位 (0 单独). 量化前用最大的参数值作为scale进行归一化. 为了进一步减少内存, 对 scale 也进行量化. 即两阶段的量化. FT 时, 前向、反向传播时, 对 scale 和 weight 依次反量化计算激活值, LoRA 的参数是 BF16 的, 梯度下降只对 LoRA 做. 在资源受限时, 增加参数、降低精度是有利的.

Reinforcement Learning

强化学习, 策略函数 (Policy), 奖励函数 (Reward), (状态)价值函数 (Value):

• 策略函数 ($\pi$), 根据当前状态 (State) 生成下一步动作 (Action) 的概率分布;
• 奖励函数, 根据当前状态 (State) 生成下一步动作 (Action) 的奖励;
• 价值函数, 根据当前状态 (State) 以及策略 (Policy) 输出按当前策略奖励的期望.

常见的三类基于深度学习的强化学习方法:

1. 基于价值函数的方法 (e.g., DQN): 通过神经网络学习价值函数, 输入当前状态, 直接输出所有动作最终能够得到的价值 (离散情况; 连续情况则输入还要输入动作), 选择价值最大的作为下一步动作;
2. 基于策略函数的方法 (e.g., REINFORCE): 通过神经网络学习策略函数, 输入当前状态, 输出下一步动作的概率分布, 通过最大化价值优化动作分布, 在优化过程中价值以估计的方法计算 (e.g., 蒙特卡洛方法);
3. Actor-Critic方法 (e.g., PPO): 同时学习策略和价值函数, 本质上是基于策略的方法, 不过是用可学习的网络代替了估计方法来计算价值而已. 策略和价值网络产生 Loss 的方式不同:
   • 价值网络: 一般采用时序差分算法, 该算法的核心思想在于, 在最优策略下, (当前状态的价值) 与 (当前状态下采用行动的奖励+衰减因子*下一状态的价值) (即时序差分项) 是相等的, 于是价值函数就是要优化网络, 使得:$$\mathcal{L} _{v}=\argmin[r _t+\gamma V _{\theta}(s _{t+1})-V _{\theta}(s _{t})]$$最小. 其中 $r _t$ 是当前状态采用的行动的奖励, $\gamma$ 是衰减因子. 注意, 此时时序差分项不会产生梯度, 是被作为 Ground Truth 的.
   • 策略网络: 策略网络的核心诉求是最大化价值, 但实际计算起来可视为一种特殊的交叉熵损失:$$\mathcal{L} _p=\argmin[-(\log\pi _\theta(s _t)) _{a _i}\cdot\mathcal{L} _v.detach()]$$ 其中前项是采取动作 $a _i$ 的熵. 与普通交叉熵不同的是, $\mathcal{L} _v$ 控制了交叉熵梯度更新的方向, 即: 当采取行动 $a _i$ 会使得下一个状态不是最优状态 ($\mathcal{L} _v$ 为负) 时, 说明应该降低 $a _i$ 发生的概率, 因此进行的是梯度上升; 反之, 即为普通交叉熵的情况, 执行梯度下降.

PPO (Proximal Policy Optimization)

PPO 属于 Actor-Critic 类的强化学习算法. 前面描述的 Actor-Critic 用的是最经典的策略梯度算法, 其缺点在于训练不稳定、策略梯度的更新不可控, 即我们无法保证每次的梯度更新得到的都是更好的一个策略. 对此, TRPO (Trust Region Policy Optimization) 提出了信任区域 (Trust Region), 以确保在该区域更新策略能带来正向优化. PPO 是 TRPO 的简化版, 其以惩罚或截断的方式代替了信任区域, 以保证新参数与旧参数差距不会过大. PPO 在绝大多数情况下比 TRPO 快、效果好.

OAI 的 RLHF (Reinforcement Learning with Human Feedback) 用的是 PPO-截断:

$$
\mathcal{L} _p^{PPO}=\argmax[\mathbb{E} _{q\sim P(Q), o\sim\pi _{\theta _{old}}(O|q)}\frac{1}{|o|}\sum _{t=1}^{|o|}\min[\frac{\pi _\theta(o _t|q,o _{<t})}{\pi _{\theta _{old}}(o _t|q,o _{<t})}A _t,clip(\frac{\pi _\theta(o _t|q,o _{<t})}{\pi _{\theta _{old}}(o _t|q,o _{<t})},1-\epsilon, 1+\epsilon)A _t]]
$$

其中, $\pi _\theta$ 和 $\pi _{\theta _{old}}$ 分别是当前策略和过去的策略, 添加这一项可以保证无偏 (期望不变) 的同时采用过去策略与环境互动的数据进行训练, 从而避免每次训练前都要先用当前策略与环境互动得到训练数据, 即由 (On-Policy -> Off-Policy). 无偏是因为:

$$
\mathbb{E} _{(o,q)\sim\pi _\theta}f(o,q)=\int\pi _\theta(o,q)f(o,q)d(o,q)=\int\frac{\pi _\theta(o,q)}{\pi _{\theta _{old}}(o,q)}f(o,q)\pi _{\theta _{old}}(o,q)d(o,q)=\mathbb{E} _{(o,q)\sim\pi _{\theta _{old}}}\frac{\pi _\theta(o,q)}{\pi _{\theta _{old}}(o,q)}f(o,q)
$$

而:

$$
\frac{\pi _\theta(o,q)}{\pi _{\theta _{old}}(o,q)}=\frac{\pi _\theta(o|q)\pi _\theta(q)}{\pi _{\theta _{old}}(o|q)\pi _{\theta _{old}}(q)}\approx\frac{\pi _\theta(o|q)}{\pi _{\theta _{old}}(o|q)}
$$

上式成立因为假设不同策略看到的状态 (对 LLMs 即 q) 分布相似. 另一种是 PPO-惩罚, 即将前后策略输出分布的KL散度加入损失项中, 不常用.

$A _t$ 的计算

$A$, 即优势 (Advantage), 代表当前动作优于平均水平的程度. 如果只看一步的优势, 那么 $A _t$ 即等于时序差分误差项:

$$
A _t = \delta _t= r _t+\gamma V _{\theta}(s _{t+1})-V _{\theta}(s _{t})
$$

若考虑未来所有步的优势, 则采用广义优势估计 (Generalized Advantage Estimation，GAE):

$$
\begin{align*}
A _t^{GAE}&=(1-\lambda)(A _t^{(1)}+\lambda A _t^{(2)}+\lambda^2 A _t^{(3)}+...)\
&=(1-\lambda)(\delta _t+\lambda (\delta _t+\gamma\delta _{t+1})+\lambda^2 (\delta _t+\gamma\delta _{t+1}+\gamma^2\delta _{t+2})+...)\
&=\sum _{i=0}(\gamma\lambda)^i\delta _{t+l}
\end{align*}
$$

即越后面的动作产生的优势受当前动作的影响越小, 因此在计算从当前开始到最后的优势时, 要对后面的优势进行衰减. 注意, $A$ 是用旧策略计算的.

$\gamma$ 的取值, 过大会带来高方差, 但是是 $\gamma$ 的准确估计; 相反, 过小 方差低, 但不准; $\lambda$ 一样

PPO 与 RLHF

Fig. 8. PPO

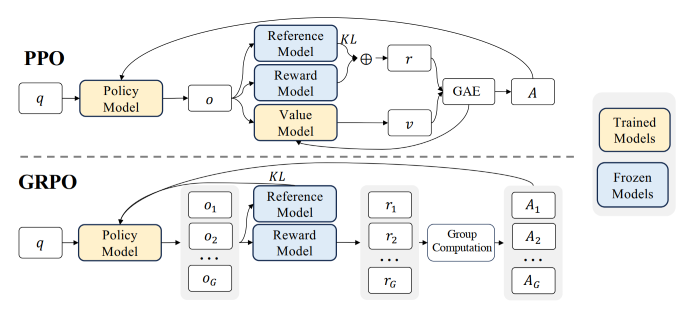
对于一些难以明确定义 Reward 的文本生成问题, 如写诗、写小说等, 为了免除繁重的人工评判, 需要预先训练一个奖励模型, 因此 PPO feat. RLHF 用到的模型有四类:

• Policy Model: 即需要训练的LLMs;
• Value Model: 即价值模型;
• Reward Model: 即用 Human Feedback 数据训练的奖励模型;
• Reference Model: 即参数冻结的LLMs (Pretrain+SFT 后的, 即 Policy 的初始参数), 保证 RLHF 后的参数不会偏离初始参数太远.

虽然表面上有 4 个模型, 但实际上用 Human Feedback 数据训练的奖励模型会在 PPO 的过程中同时充当 Reward 和 Value Model (好像不一定? 以前的 TRL 的 Value Model 是在 Policy 加个投影头), 只不过 Reward Model 被冻结而 Value Model 会在 PPO 过程中被更新. 类似地, Policy 和 Reference 也是同一个模型, 只不过 Reference 被冻结而 Policy 可训练 (Policy_old 直接记录以前的输出即可). 整个过程中, 最重要的一点就是: 我们只优化两个模型-- Policy and Value. Policy 本质是在做一个分类任务, Value 本质是在做一个回归任务, 因此, 只有将旧有策略交互得到的 Prompts+Responses 输入的那一步出来的值需要梯度, 即分别是 Policy 和 Value 的输出. 基本的流程如下:

Fig. 9. PPO Pipeline

1. Training Reward Model with Human Feedback. RLHF 的第一步, Reward Model 接受 Prompt+Response (B, L, D), 输出 (B, L) 的向量, 其中在 L 维度上, 第 i 位置表示 i 这个状态 (token) 能获得的奖励和 (即价值), 供 Value Model 使用; 最后一个位置的值则表示对整个句子的打分, 供 Reward Model使用. 训练时采用 Pair-wise Loss, 即同时接受人工排序好的两个句子, 提高好句子 (chosen) 的打分, 而降低差句子 (rejected) 的打分:

   # code
   chosen_reward = reward_model(chosen)[:, last_non_pad_token_chosen]
   rejected_reward = reward_model(rejected)[:, last_non_pad_token_rejected]
   loss = -torch.log(F.sigmoid(chosen_reward - rejected_reward)).mean()  # 将 chosen 视作正例

2. Interact with Environment and Generate Data (PPO Step 1). 旧策略与环境交互, 生成训练数据:

   # code
   with torch.no_grad():
       # 等价于强化学习的交互阶段, 用旧策略生成训练数据.
       # (B, L) -> (B, L+H)
       query_responses, logitss = policy_model.generate(prompts)

3. Rating and Calculate Rewards, Values, Advantages (PPO Step 2). 随后, 用训练好的 Reward Model 在初始化一个 Value Model, 并冻结 Reward Model 的参数. Reward 和 Value Model 分别打分, 进一步计算 advantages:

   # code
   with torch.n _grad():
       logits = logitss[:, only_consider_responses]                            # 只考虑回答的部分
       _, logits_ref = ref_model(query_responses)[:, only_consider_responses]  # 用于约束训练后模型分布不会太偏离未训练模型
       log_prob = selective_log_softmax(logits)                                # 注: 此时已做出动作选择, 即 log_prob 的维度是 (B, H)
       log_prob_ref = selective_log_softmax(logits_ref)
       # 起约束作用的 KL散度
       kl_divergence = -beta * (log_prob - log_prob_ref)     # beta 为约束系数
   
       # (B, L+H) -> (B, 1), 打分, 输出 r _\phi
       reward_scores = reward_model.get_reward(query_responses)
       # 加上KL散度约束的最终 reward
       rewards = kl_divergence + reward_scores  # 需要注意, responses 的每个位置都有 KL 约束, 但是 reward_scores 只加在最后一个位置
       # (B, L+H) -> (B, L+H-1)
       values = value_model.get_value(query_responses)[:, :-1]
   
       # 根据 values 和 rewards 计算 advantages 和 时序差分项: r + V(s+1) = A + V(s), 记作 return
       lastdelta = 0
       advantages_reversed = []
       length = rewards.size()[-1]
       # 计算每个时刻的优势, 同样只考虑 responses 部分
       for t in reversed(range(start, length)):
           nextvalues = values[:, t + 1] if t < length - 1 else 0.0
           # A = delta = r + \gamma V(s+1) - V(s)
           delta = (rewards[:, t] + gamma * nextvalues) - values[:, t]
           # gamma, lam 两个衰减因子
           lastdelta = delta + gamma * lam * lastgaelam
           advantages_reversed.append(lastgaelam)
       # r + V(s+1) = A + V(s)
       returns = advantages + values[:, start:]

4. Calculate Loss, Update Policy and Value Model (PPO, Step 3). 计算 Loss, 梯度下降:

   # code
   # 新策略与老策略初始化相同, 此处开始不相同, 因为要更新新策略 num_ppo_epochs 次.
   logits_old = 
   for _ in range(num_ppo_epochs):
       # policy loss, 策略的损失
       new_log_prob = selective_log_softmax(policy_model(query_responses))
       ratio = troch.exp(new_log_prob - log_prob)
       p_loss_1 = - ratio * advantages
       p_loss_2 = -advantages * torch.clamp(ratio, 1.0 - cliprange,
                                               1.0 + cliprange)
       p_loss = torch.max(p_loss_1, p_loss_2)  # 因为带了负号, 所以取 max
       
       # value loss, 价值的损失: r + V(s+1) - V(s)
       new_values = reward_model(query_responses)[:, :-1]
       # 对 value 也裁剪, 使其不至于偏离原模型过多
       new_values_clipped = torch.clamp(
                                   new_values,
                                   values - cliprange_value,
                                   values + cliprange_value,
                               )
       v_loss_1 = torch.square(new_values - returns)
       v_loss_2 = torch.square(new_values_clipped - returns)
       v_loss = 0.5 * torch.max(v_loss_1, v_loss_1)
   
       loss = p_loss + v_coef * v_loss
   # 极简版, 所有的 Loss 都只对 Responses 的 Token 求.

补充: 加入与参考模型 KL散度 (此处实际就是生成 o_t 的概率比) 后的 reward 计算:

$$
r _t = r _\phi(q, o _{\le t})-\beta \log\frac{\pi _{\theta _{old}}(o _t|q,o _{<t})}{\pi _{\theta _{ref}}(o _t|,o _{<t})}
$$

即偏离 ref 太远 reward 会下降.

问答

1. PPO 过程中, reward model 会有什么问题?

reward model 的准确率会逐渐下降. 因为 reward model 毕竟只是用有限的数据训练出来的, 一般来源于 sft 模型的回答, 因此在 PPO 的过程中, 当模型逐渐偏离 sft 模型, 开始输出一些 reward model 没见过的 OOD 回答时, reward model 的有效性就会下降. 且也可能出现一种情况是, 模型在 PPO 过程中找到了一条捷径, 就是一些对人来说可能没有意义的输出 reward model 会给很高的分数, 最终的结果就是 PPO 训练失败了. 所以 RLHF 的训练步数不能很长.

2. 对上面的问题除了少训练点还有什么解法吗?

Llama 2 用的方法是训练一段时间后, 从训练后的模型在采样一些 pair, 重新训练 rm, 就是比较麻烦.

3. 现阶段能跳过 SFT 直接 RLHF吗?

当前来说不行. 直接 RLHF 的搜索空间太大, 成本过高, 且需要有一个天然的、准确的 reward model, 而这在语言中, 除了像数学题、编程题这种有明确评判标准的, 其他的 reward model 构建都需要极大的成本. 所以需要先 SFT 来缩小搜索空间.

4. PPO 为什么在初始阶段会先把 actor model 冻结?

为了单独训练 value model. 进而稳定后续 actor model 的学习.

5. PPO 稳定训练 trick.

a. 训练 reward model 的时候加入对好样本的 pretrain loss (CE). b. reward 归一化 (mean, std) 与裁剪, advantage 与 reward 相关, 所以不用特别操作 (已融入 trl 中). c. token wise kl-penalty, 也已经融入 reward 的计算中. c. value model 要先训练一段时间再训练 actor, 至于 value model 用 actor 还是 reward 初始化区别不大. d. actor 的训练中也加入 pretrain loss. e. reward model 训练时 L2 正则, 防止 BT 只优化正负例的距离. f. 动量更新 reference model, 大 batch size.

6. PPO 训崩了有什么迹象?

PPO 崩溃最主要的情况是 reward hacking, 即模型找到了一个可以让 reward model 打很高分数, 但是对人来说没有任何意义的输出. 具体表现为: reward 骤增, KL 骤增, PPL 骤降, 回答长度骤增.

7. RLHF 的上界?

是 reward model 的上界, 即在 rm 下 best-of-N 的上界. 因为 rm 处理的是评判任务, 而 actor 处理的是生成任务, 评判任务本身就比生成简单, 所以 rm 在评判任务上能学得更好, actor 是根据 rm 的反馈学习的, 那么 rm 反馈准确率的上界也就是 rlhf 的上界了.

8. DPO、PPO 解码策略对结果的影响

DPO 因为优化整体, 没有 Token-wise 的优化, 所以greedy效果不如 PPO, 因为某些关键的 Token 未必被优化地概率很高, 但相应地 top _p效果还不错; PPO 存在 Token-wise 的优化, 因此有利的 Token 会被增强, 但同样地和有利 Token 很像的也会被增强, 所以 top _p反而没那么强.

9. Llama 多阶段 RLHF 的 reject sampling

即在 RLHF 过程中, 会隔段时间让模型生成 k 个答案, 选择 reward model 打分最高的对模型 SFT. 目的是让模型能学到更多样的东西, 一定程度上是在拟合 rm 的 BoN.

DPO

将 Reward Model 对大模型在相同 prompt 下的两个回答好坏的评判视作 Bradley-Terry Model 的过程, 即将 Reward Model 视作"实力"的参数, 此时 $r(prompt, response)$ 输出的就是大模型这段回答的"实力". 最终的损失函数为:

$$
\mathcal{L} _{dpo}=-\mathbb{E} _{(p, o _w, o _l)\sim D}[\log\sigma(\beta\log\frac{\pi _\theta(o _w|p)}{\pi _{ref}(o _w|p)}-\beta\log\frac{\pi _\theta(o _l|p)}{\pi _{ref}(o _l|p)})]
$$

其中 $\pi _\theta(o _w|p)$ 为对 Ground Truth 预测概率的和 (整条 Response 序列), 这实际上将 RLHF 转化为了一个类似二分类的监督学习问题.

Bradley-Terry Model: 一种体育比赛的统计模型, 用参赛队伍两两之间的胜负关系来估计队伍的实力, 进而对未曾交手的两支队伍的胜负进行预测. 该模型认为每只队伍都有一个固定的参赛水平, 对于水平分别为 a 和 b 的两支队伍, 两者交手, a 的胜率为 a / (a+b), b 的胜率为 b / (a+b). 由此, 根据队伍已有的交手记录, 我们可以得到若干队伍间交手胜率的观测值, 然后使用 MLE 就可计算出每支队伍的实力.

问答

1. DPO 第 0 步的 loss 固定吗?

固定. 因为此时模型和 ref 一模一样, 故 sigmoid 的值为 0.5, 取 log 是 0.693

2. DPO 在学习过程中 positive 和 negative 的概率同时下降?

因为 DPO 优化的是 positive 和 negative 之间的 gap. 所以如果 positive 和 negative sample 的大部分 token 是一致的, 那么 DPO 很难学到 positive sample 中的模式, 因为 BT loss, Bradley-Terry loss 只优化两者间的 gap, 对此, DPO 找到的捷径就是同时降低 negative 和 positive sample 的概率.

3. DPO 训练后模型为什么输出越来越长?

这和数据集有关. 正例往往更长, 所以 DPO 就会倾向于输出更长的文本.

4. 什么是 Pair RM?

原本 RM 看到的是 (prompt, answer), Pair RM 看到的是 (prompt, pos _answer, neg _answer). 这样首先是效率高点, 然后正负例可以看到对方, 模型可以将两者对比着学习, 整体的解释性和泛化性会比一般的好. (原始 RM 容易 overfit)

5. BT model (DPO, RM) 的不足

只学习两两间的局部关系, 无法学习全局关系; 容易过拟合字面上差距大的正负例对; 模型只学习到了正例, 对负例输出的概率接近 0, 鲁棒性差.

6. DPO 的变体有哪些?

DPO 容易过拟合数据集. IPO: $\argmin (\log\frac{\pi(y _w|x)\pi _{ref}(y _l|x)}{\pi(y _l|x)\pi _{ref}(y _w|x)}-\beta)^2$, 相当于加入 L2 正则, 保证 DPO 不使用 Early stop 的收敛性.

GRPO

Fig. 10. PPO v.s. GRPO

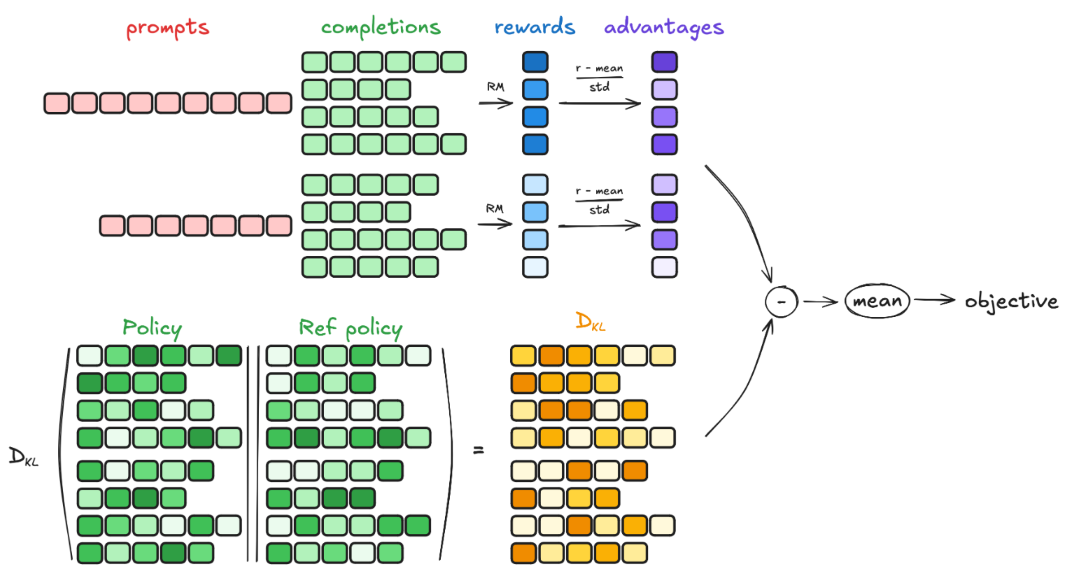
PPO 需要知道从当前步开始的最终奖励以估计 $A$, 因而 PPO 会需要一个 Value Model 来估计奖励. GRPO 则通过对同一个 prompt 生成多个回答 $o _i$, 然后用这些回答的总体评价 $r _i$ 作为整个回答的价值 $v _i$, 来省去价值函数, 最后用所有回答的均值和方差对每个回答进行标准化, 来达到类似 GAE 的效果:

$$
A _i = \frac{r _i-\text{mean}(r)}{\text{std}(r)}
$$

直观地来讲就是: 把 LLM 响应的过程只当作一个 Action, 那么此时的 $r$ 就是实际上的 $v$.

最终的损失函数为:

$$
\mathcal{L} _{grpo}=\argmax[\mathbb{E} _{q\sim P(Q), o\sim\pi _{\theta _{old}}(O|q)}\frac{1}{G}\sum _{i=1}^{G}\frac{1}{|o _i|}\sum _{t=1}^{|o _i|}\min[\frac{\pi _\theta(o _{i,t}|q,o _{i,<t})}{\pi _{\theta _{old}}(o _{i,t}|q,o _{i,<t})}A _i,clip(\frac{\pi _\theta(o _{i,t}|q,o _{i,<t})}{\pi _{\theta _{old}}(o _{i,t}|q,o _{i,<t})},1-\epsilon, 1+\epsilon)A _i]-\beta\mathbb{D} _\text{KL}\left[\pi _\theta|\pi _{\text{ref}}\right]]
$$

或者 $\log\frac{\pi _\theta(o _{i,t}|q,o _{i,<t})}{\pi _{\theta _{old}}(o _{i,t}|q,o _{i,<t})}$, 这样除就变成减了. 上式与 PPO-惩罚基本一致.

其中 $G$ 是每个 prompt 生成的回答个数 (即 Group 的由来), $|o _i|$ 是每个回答的长度. 最后的 KL 约束项是为了防止最终模型偏离初始模型过远. GRPO 对 KL 约束项的计算也是采用估计的方法, 只不过和 PPO 的不同:

$$\mathbb{D} _{\text{KL}}\left[\pi _\theta|\pi _{\text{ref}}\right] = \frac{\pi _{\text{ref}}(o _{i,t} \mid q, o _{i,<t})}{\pi _\theta(o _{i,t} \mid q, o _{i,<t})} - \log \frac{\pi _{\text{ref}}(o _{i,t} \mid q, o _{i,<t})}{\pi _\theta(o _{i,t} \mid q, o _{i,<t})} - 1, $$

此处计算的 KL 是把当前的 policy $\pi _\theta$ 当作真实分布的, 但由于参数是可更新的, 所以实际上是在限制当前的策略不要偏离 ref 的太远. 上式为凸函数 (开口向上), 所以, 因为最后是梯度下降, $\mathcal{L} _{grpo}$ 还要乘负号, 故对 $D _{KL}$ 的优化是向最小值的.

计算流程如下:

Fig. 11. GRPO

问答

1. KL 散度的估计方式?

设真实分布为 q, 用来近似真实分布的分布为 p. k1 估计: $\log\frac{q(x)}{p(x)}=-\log\frac{p(x)}{q(x)}$, 无偏, 但是方差大, 因为有一半可能为负值, 但KL一定为正值; k2 估计: $\frac{1}{2}(\log\frac{q(x)}{p(x)})^2$, 有偏, 但方差小, 因为始终为正; k3 在 k1 的基础上得到, 他在 k1 上加了一个期望为 0 (关于 $q(x)$) 且与 k1 负相关的量, 从而在保证无偏的同时降低方差. 即 $\frac{p(x)}{q(x)}-1$, 这样有一个很美好的性质: $x-1\ge \log(x)$, 所以 $\frac{p(x)}{q(x)}-1-\log\frac{p(x)}{q(x)}$ 恒正!

2. 为什么要估计 KL 而不是直接算?

太耗资源, 需要很多的 sample. 所以只能用少量的样本估计.

3. Dense Reward

类似于 code 和 math 过程分, GRPO dense reward 更好, 鼓励模型探索难题.

Fig. 12. DeepSeek-R1 Pipeline

随想

• DPO 和 PPO 的区别与联系. 从目的上的来讲, 大语言模型的强化学习都是要优化模型使得模型能够输出符合人类偏好的输出, 所以最基础的损失函数就是: 给定两个问答 Pair, 一好一坏, 模型在好回答上的 reward 更高. 为了实现这一目标, DPO 是把模型的整个回答视作一次 Action, 因而是一个将该问题转化为了一个特殊的多臂老虎机的问题, 然后又通过转换建立的 Reward 和 Policy 的关系, 从而实现将 LLM 同时视作 reward 和 Policy model, 最大化正例, 最小化负例, DPO 实现的是利用 正例和负例 的对比来优化模型. 他对 reward 是采用样本的观测值来估计的, 或者说是 概率 这一个特殊的 reward 来估计的. 所以就本质上来说, DPO 需要很多的训练样本, 这样统计上估计的 reward 才能够逼近期望; PPO 则是把每次 Next token prediction 视作一次 Action, 因而生成整个回答的过程是个 马尔可夫决策过程, 相应地需要过程的 reward, 然后是直接最大化 reward, 而不是直接将正负例对比地学. 不同于 DPO, PPO 会首先学习一个 reward model 来对 respond 打分, 而不需要很多的样本的平均值做估计, 因此样本效率更高, 但相应地, reward model 毕竟也只是用数据优化的模型, 而不是一个真正地能够完全反映人类偏好的 model, 所以 PPO 在优化的过程中会很容易找到一条捷径, 即 reward hacking, 这时 模型输出的实际是对人没有任何意义的东西, 如一直重复某个词, 但 reward model 却会给其打高分.

• DPO 高方差 (无价值函数、离线 (数据无法及时更新, 随着训练进行, 与当前的分布差异越来越大)); PPO 低方差 (引入 value model, 有着更准确的价值估计.)

• FA1 和 FA2 的区别: 减少了 Output 的写入次数, FA1 的外层循环 Load K, V, 内层 Load Q, O; FA2 的外层循环 Load Q, 内层 Load K, V. 所以对于 FA2, 一轮内部训练可以把一 block 的 Q 的结果都计算出来, 因而 FA2 在计算的时候可以把 前面的 在 SRAM 里存着; 而 FA1, 由于对于同一个 BLOCK 的 kv, 内部是先计算不同 Block 的 Q, 得到 O, 而此时的 O 是不完整的, 因为只使用了部分的 kv, 所以为了处理下一个 BLOCK 的 Q, 必须要把这个 O 给写入 HBM, 这就增加了 IO.

• 先切分流水并行，然后张量并行是相邻的卡，剩下的做数据并行。