Retrievers: Indexing and Ranking
每次临近毕业都是很闲的时候,因此如本科毕业般,这次也想学点之前没认真学的东西。召回、各类大模型技术报告、新的语言......那么先从召回开始。
从盘古开天地看起也不太现实,所以主要是围绕几篇主要的论文展开:
- Hierarchical Navigable Small World (HNSW)
- Tree-based Deep Models (TDM)
- Deep Retrieval (DR)
- NANN (二向箔)
- Trinity
- Streaming VQ
- MERGE
HNSW
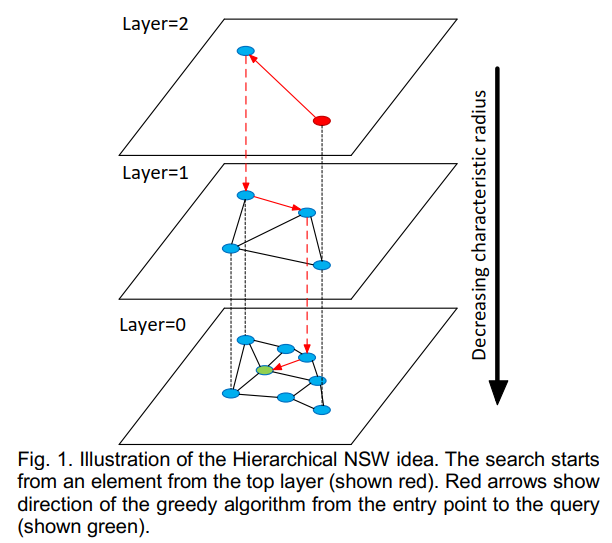
HNSW(Hierarchical Navigable Small World)是工业界最常用的向量检索结构之一。正如其名称所示,它通过构建多层级的小世界图来实现高效的近邻搜索。从直觉上看,HNSW 可以被类比为一张“谷歌地图”:当我们试图在地图上寻找某个具体街区时,通常会先在较粗的尺度上定位国家或城市,再逐步放大视图,最终在高分辨率的局部区域中完成精确定位。类似地,HNSW 的搜索过程也是一个由粗到细的逐层导航过程:高层图中节点稀疏、连接跨度大,用于快速确定查询向量所在的大致区域;随着搜索逐层下沉,图结构逐渐变得更加稠密,从而在局部范围内进行更精细的近邻探索。
由此我们可以看到,HNSW只是index,它由Item Embedding离线构图,Serving时给定seed从上层的最近邻一路索引到最下层的最近邻,而ranking由双塔模型承担。
Training
Training不涉及任何HNSW,只训练双塔(U侧塔,G侧塔)。
Offline Graph
HNSW为层次级的向量索引结构,给定层高决定系数$m _L$,索引的最大连接数$M _{max}$,以及构图索引的基础连接数$M$,HNSW以逐节点插入的方式构图,而最终的检索则可视为在$L _0$插入节点。
KNN-search
HNSW的检索是近似KNN(AKNN)检索,给定Query(User Embedding或者Item Embedding)以及K(返回结果个数),KNN-search可归结为:
- 从$L _{max}$开始,给定enter point(ep,一般为度最大的节点),执行Search_Layer(ef=1),即分别与ep、ep的邻居求欧式距离,找到最近的点$e _{Lmax}$,加入候选集$W$,同时以$e _{Lmax}$为ep,进入下一层$L _{max-1}$;
- 在$L _{max-1}$~$L _1$,重复1的操作,此时候选集$W$的元素为{$e _{Lmax},e _{Lmax-1},...,e _{L1}$};
- 从$e _{L1}$进入最底层$L _0$,执行Search_Layer(ef=K),即检索K个最近邻,加入$W$;
- 将从$W$中与Query最近的K个弹出,即为最终结果。
显然地,$W$会被实现为一个优先级队列,且为小根堆,而要保证上层元素一定会出现在下层,则需要构图方式保证,见后文。
Insert
Insert是HNSW构图时的唯一操作,给定$m _L$、$M _{max}$、$M$、当前最大层高$L _{max}$以及新插入元素$q$,Insert的过程为:
- 按$\lfloor-\ln(unif(0...1))\cdot m _L\rfloor$生成新插入元素的层高$L$;
- 若$L < L _{max}$,则执行Search_Layer(ef=1)一路到$L$层,并将过程中的ep加入候选集$W$;
- 在之后的每一层,先Search_Layer(ef=efConstruction),其中efConstruction为可调参数,插入$W$,再从$W$中选择$M$个候选Select_Neighbours(q, W, M),与$q$连边,作为$q$的邻居,若连边后,候选的邻居数大于$M _{max}$,则单独对这些候选重选邻居,限制其最大邻居数为$M _{max}$。
不难看出,在$L$~$0$层,每一层都会插入新节点$q$并且为其连边,所以上层有的节点下层一定有,反之不然。
Search_Layer
给定要检索的近邻个数ef,新插入节点$q$以及ep,Search_Layer是HNSW最基础的步骤:
- 初始化两个优先级队列$W$与$C$,其中$W$为大根堆,$C$为小根堆,同时维护访问过的节点表$V$,三者均初始化为ep;
为何$W$是大根堆,而$C$是小根堆?因为$W$是最终的返回结果,所以当$|W|>ef$的时候要弹出距离最远的,故要实现为大根堆;$C$是候选集,我们每次肯定是贪心地插入最近的,所以$C$要实现为小根堆,以弹出最小的。因此整个Search_Layer就是一个遍历$C$的过程,遍历的终止条件为$C$为空或者$C$中的最小值已经大于$W$中的最大值。
- 对$C$中当前的最小元素$c$,若其不满足上面所说的终止条件,则遍历$c$的邻居,更新访问节点表$V$,将可插入$W$的邻居插入,保持$|W| <= ef$,在插入$W$的同时插入$C$;
为何不考虑$c$?a. 对最初的情况,因为$W$与$C$的初始化是一样的,所以ep最开始就被考虑了;b. 后续的节点都是经过2被插入到$C$的,因此能被插入的也早被插入到$W$了。
- 重复2,直到满足遍历终止条件。
Select_Neighbours
文中给了两种方式:
- Simple:就选距离最近的K个;
- Heuristic:启发式算法除了考虑距离外,还考虑了区域的连通性,即当图存在非联通子图时,还会强行地连接两个非联通子图,保证全图的连通性。
Hyper、Complexity
据文中所述,$M _{max}=2M$、$m _L=\frac{1}{\ln M}$,$M\in[5,48]$即可。构图复杂度$N\log N$,检索复杂度$\log N$。
Serving
Serving归结下来就是一个查表的过程,根据不同的Query构造方式,流程也会有些许不同:
| Query | User Embedding | 历史正向互动Item Embedding |
|---|---|---|
| Query 来源 | U侧与Context特征实时过U侧塔得到的Embedding | 离线(或实时)Embedding |
| Query 数量 | 1 个 | 多个(通常取最近 N 个) |
| 与双塔模型的关系 | 双塔直接用于召回(User→Item) | 双塔可用于对召回结果进行粗排序 |
| 与 HNSW 的关系 | HNSW 作为用户到内容的近邻搜索结构 | HNSW 作为 item-item 扩散的核心工具 |
| 与生成式视角的类比 | 使用一个全局语义 seed 进行检索 | 从多个已生成 token 出发进行扩散式检索 |
TDM
TDM(Tree-based Deep Models)算是较早的索引聚类召回。HNSW其实并没有聚类的概念,因为每个Item都是独立的索引,其以连边的方式连接了其他的Item,形成了以该Item为核心的小聚类,即我们有N个Item就有N个小聚类,而且这些小聚类还是相关联的。TDM则是通过构造虚拟节点,并将Item放在二叉树的叶子上,实现了一个层次聚类效果,大聚类->小聚类->小小聚类->Item。
Training
模型+树索引两者交替训练:
- 初始化模型、树索引(按category初始化);
- 训练模型直至收敛,其中正负样本的构造方式为:
正样本叶子的祖先均被视为正样本,相应地子节点均为负样本的节点被视为负样本
- 根据新的叶子embedding,k-means重新构造索引树(从上到下地2-means);
- 重复2~3直至收敛。
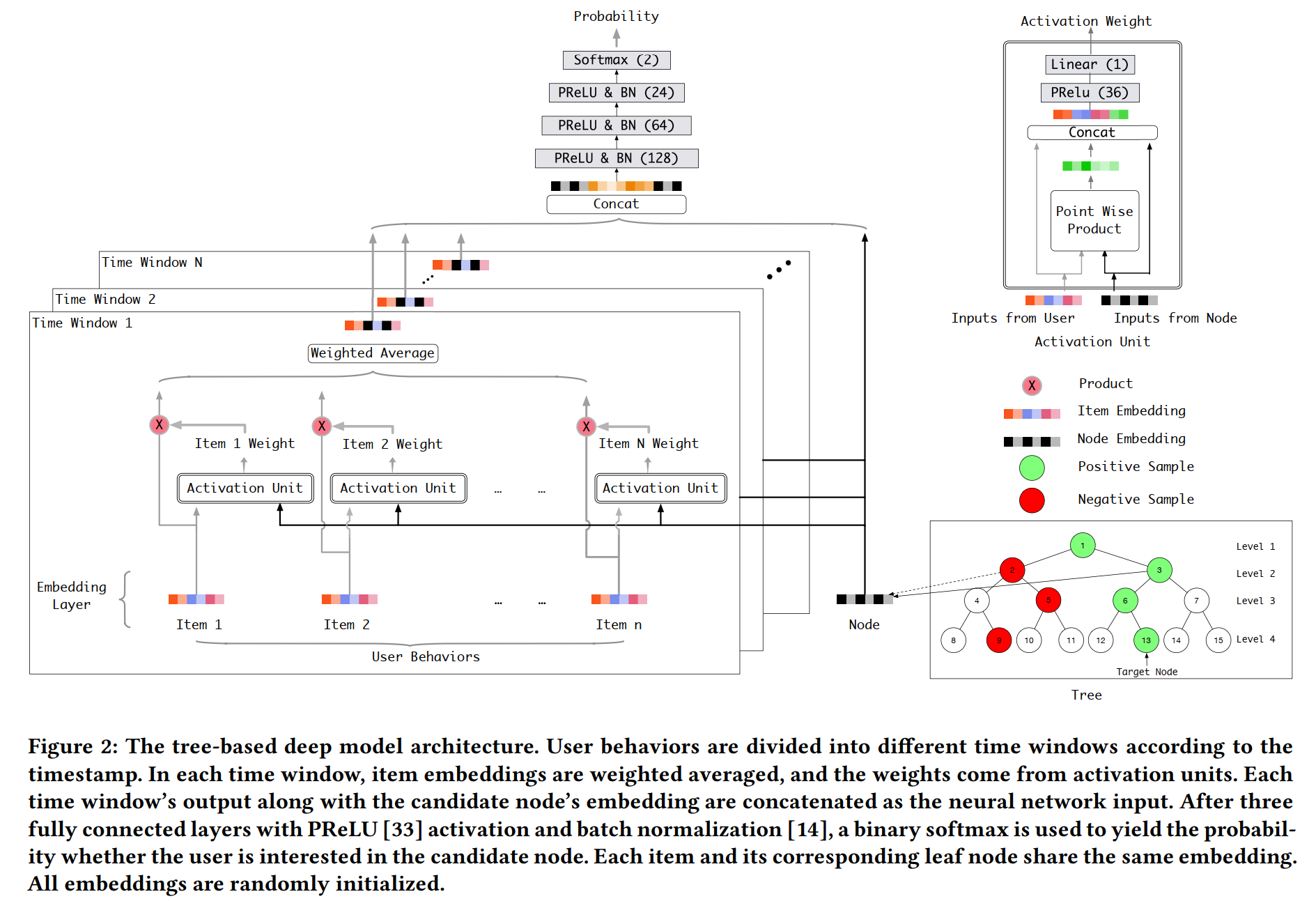
Serving
Serving就比较简单,是比较常规的Beam-Search,即:
- 所有候选节点出弹出、过模型,选Topk的子节点加入候选;
- 重复步骤1,直到叶子节点,选Topk返回。
其中,由于训练时层与层之间是没有任何累乘的条件概率制约的,即层与层之间完全不干扰,所以初始的候选应该为层节点个数>k的层的所有节点。
DR
NANN
NANN(Neural Approximate Nearest Neighbor),阿里将其简称为“二向箔”,原因在于:
- 传统的基于模型的两阶段召回,Ranking&Indexing是分开的,最终我们实际只在训练Ranking模型,而Indexing是基于Ranking模型得到的Embedding构建的,典型的如基于HNSW的召回,这导致:a. Ranking时在用U侧和G侧内积打分,Indexing时则是ANN检索,两阶段目标不一致,检索误差无法通过Ranking模型优化;b. 为了构图,Ranking模型被设计为U侧塔和G侧塔直接内积计算的模式,无法考虑更复杂的形式。不难看出,此时的召回优化,模型层面实际上是“一维”的;
- 一些一阶段的召回,如DR、TDM,将模型和索引协同训练,同时考虑模型、索引、计算,可视为“三维”。这类方式有着训练复杂度高、虚拟索引限制G侧无法利用更复杂特征的问题。
NANN是对这两者的折中,其索引退回了HNSW的形式,仍由Item embedding构图(所以两阶段召回的第二个挑战似乎不太对,换了非双塔一样可以用Item embedding建立索引),但最终检索时不再直接ANN,而是用Ranking模型对enter point的邻居打分,选topk:
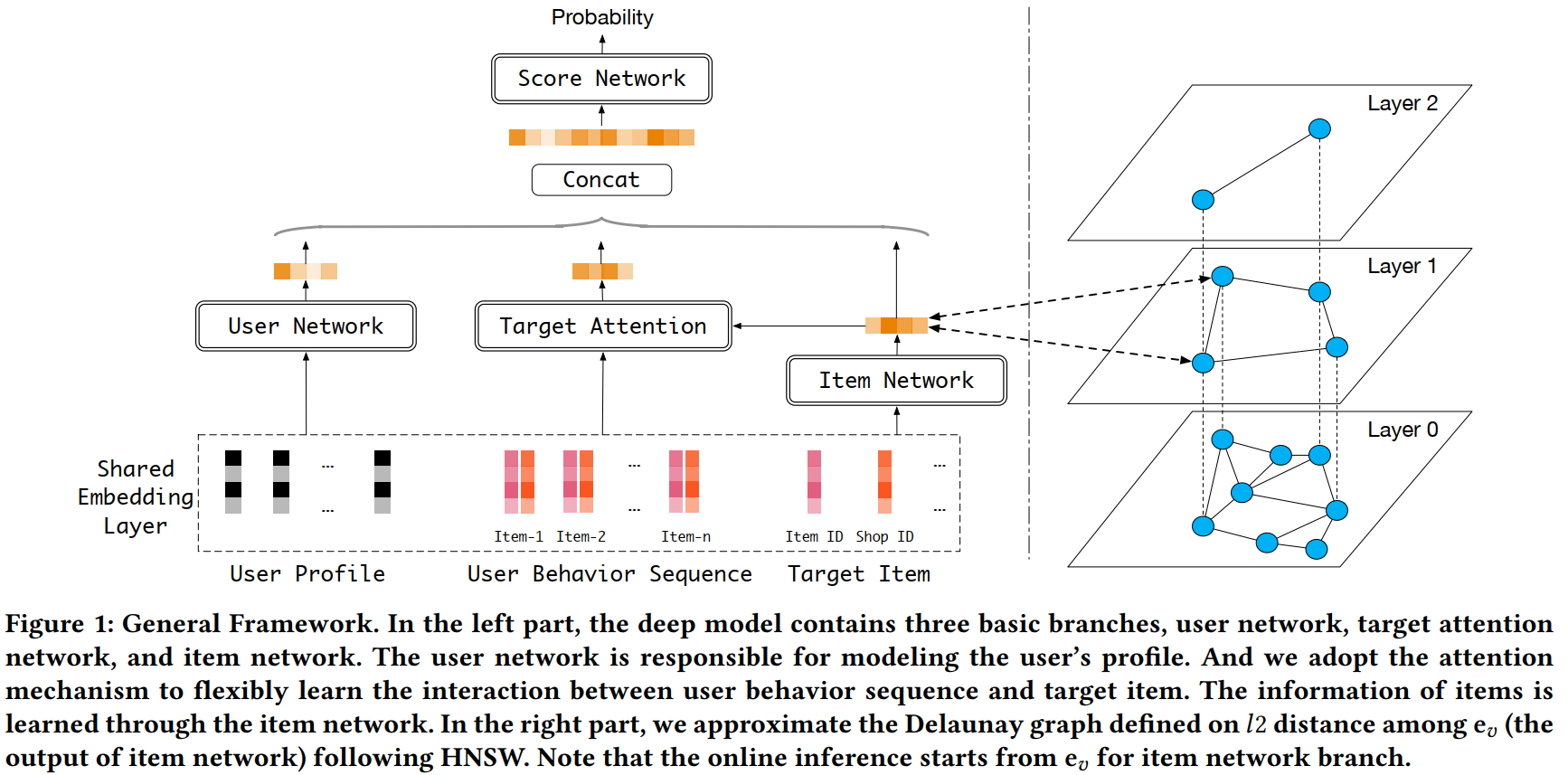
所以,名字起得很对,用Neural Network完成ANN。
Training
Training只训练Ranking模型,但由于在NANN中,HNSW构图时用的是Item embedding的ANN(且用的为欧式距离),而Serving时又用Neural Network近似这个ANN,所以还是有比较大的不一致,不过文中似乎没有详细讨论这个问题,而是将其归结为了一个鲁棒性问题:即Item embedding的一丁点扰动可能会导致结果变成一坨,因为HNSW不再用欧式距离,而是由神经网络进行打分。
文中给的方法是引入一个对抗辅助损失函数: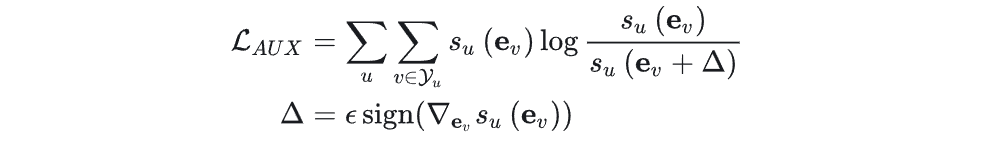
不难看到$(e _v +\Delta)$是梯度“上升”,在一定程度上可被视为Bad case。引入的辅助损失函数用KL散度约束住了Bad case。
Serving
Serving本质上是一个将ANN替换为Ranking模型打分的HNSW,即给定enter point,用Ranking模型打分邻居,选top1,进入下一层,在最下层则选topk。
Reference
Trinity
严格来说,Trinity和Streaming VQ、NANN、HNSW等不是一个类型的东西,因为后者关注Indexing+Ranking,是对整体召回流程、模型的迭代,而Trinity则是强行用某些规则、统计结果,对召回的结果进行了筛选。简单地来说,Trinity是机器学习版的纯统计的标签召回,即直接根据标签的统计结果,召回想要的视频,不过与过去的不同的是此处的标签以及聚类是VQ-VAE学习出来的,而不是人为的硬标签(如动漫、音乐等)。
因此,Trinity是对其他纯基于模型的召回的补充,它以统计的方式,缓解了各类流式更新的召回模型过于注重当下热门话题、当下兴趣的现象。
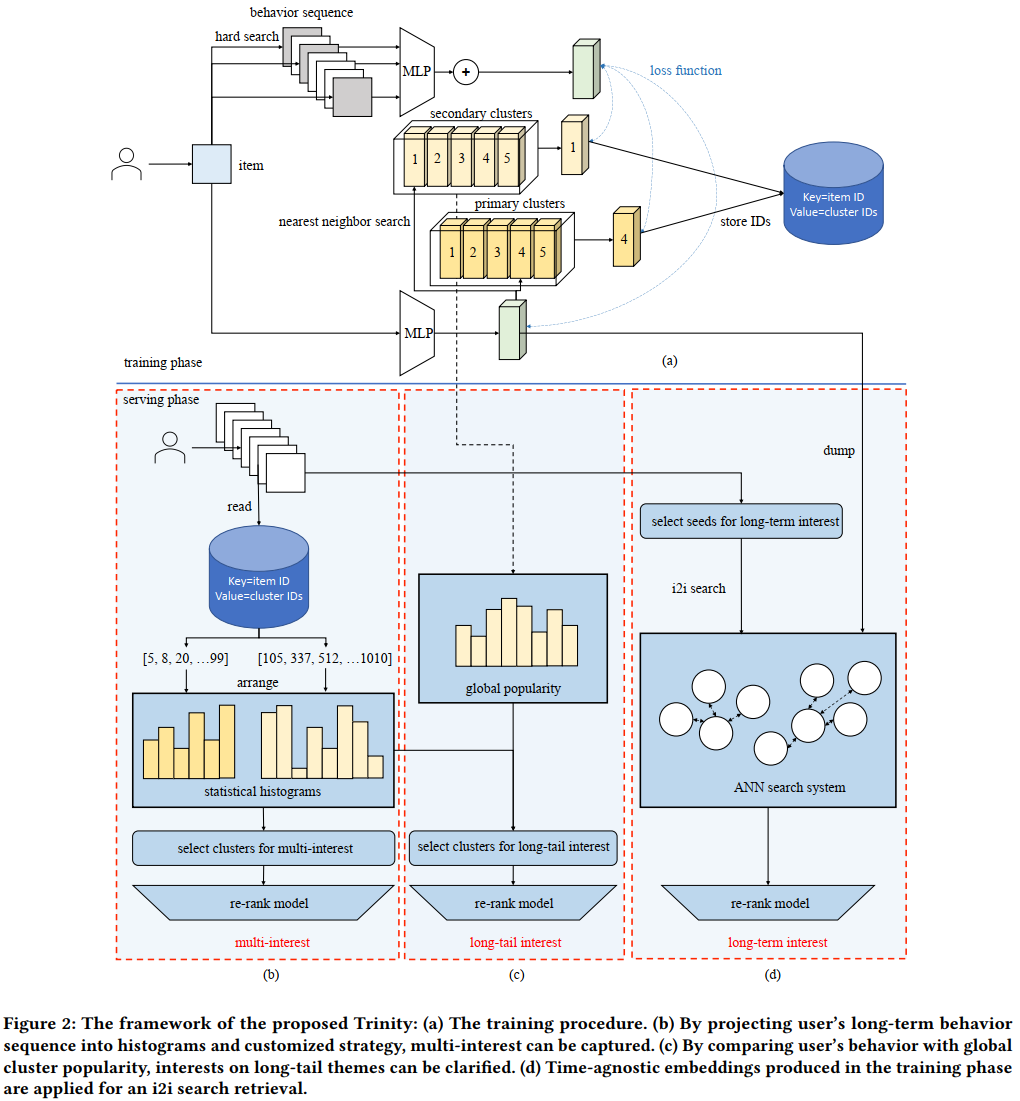
Training
Trinity的Training就只是在训练Codebook,输入为用户历史长序列以及Item,正例为互动过或者完播等的视频,与VQ-VAE、Streaming VQ基本类似。不过不同的是Trinity训练了两个Codebook,一个词本小,记为Primary Clusters;另一个词本大,记为Secondary Clusters。
Serving
Trinity的主要动机为保证用户的长期兴趣,基于此从:multi-interest(多)、long-tail interest(长尾)、long-term interest(长期),三个方面展开。
Multi-interest
- 从用户历史长序列中取互动过或者完播或者播放时长>10s的Item(Length <= 2500);
- 得到Item的Primary/Secondary Clusters,分别计算Primary Clusters和Secondary Clusters的频率直方图;
- 由于Secondary Clusters的个数多于Primary Clusters,两者存在多对一的关系,将Secondary Clusters作为Primary Clusters的子节点;
- 在频率满足阈值的Primary Clusters中,随机选一个满足频率阈值的Secondary Clusters,加入候选;
- 遍历完后候选未满则在频率满足阈值的Primary Clusters中取频率最大的Secondary Clusters,加入候选;
- 还不满则将频率大的Secondary Clusters,加入候选;
- 所有候选Item过一个Ranking模型。
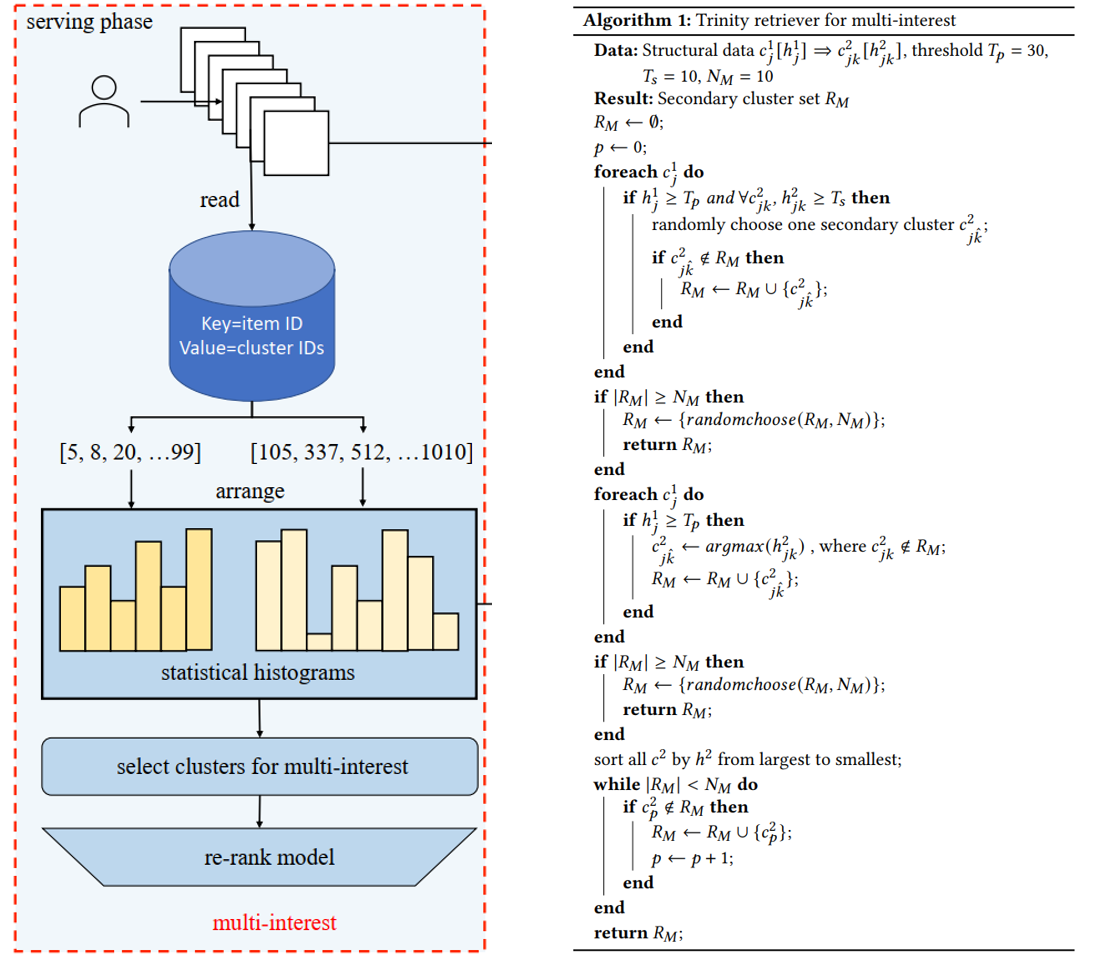
Long-tail interest
- 按Sampling Bias的方法得到每个Secondary Clusters的平均出现间隔,由大到小排序(过滤Item数过少的Clusters),取间隔最大的几个,作为全局的Long-tail interests;
- 复用Multi-interest的用户Secondary Clusters频率直方图,将频率大于阈值且在全局Long-tail interests的加入候选;
- 每个候选的Secondary Cluster以其归一化后的频率作为概率(公式见下),随机采样出限定个数的Clusters,作为最终候选;
- 所有候选Item过一个Ranking模型。
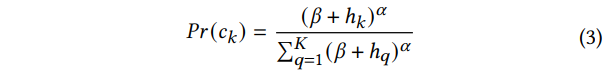
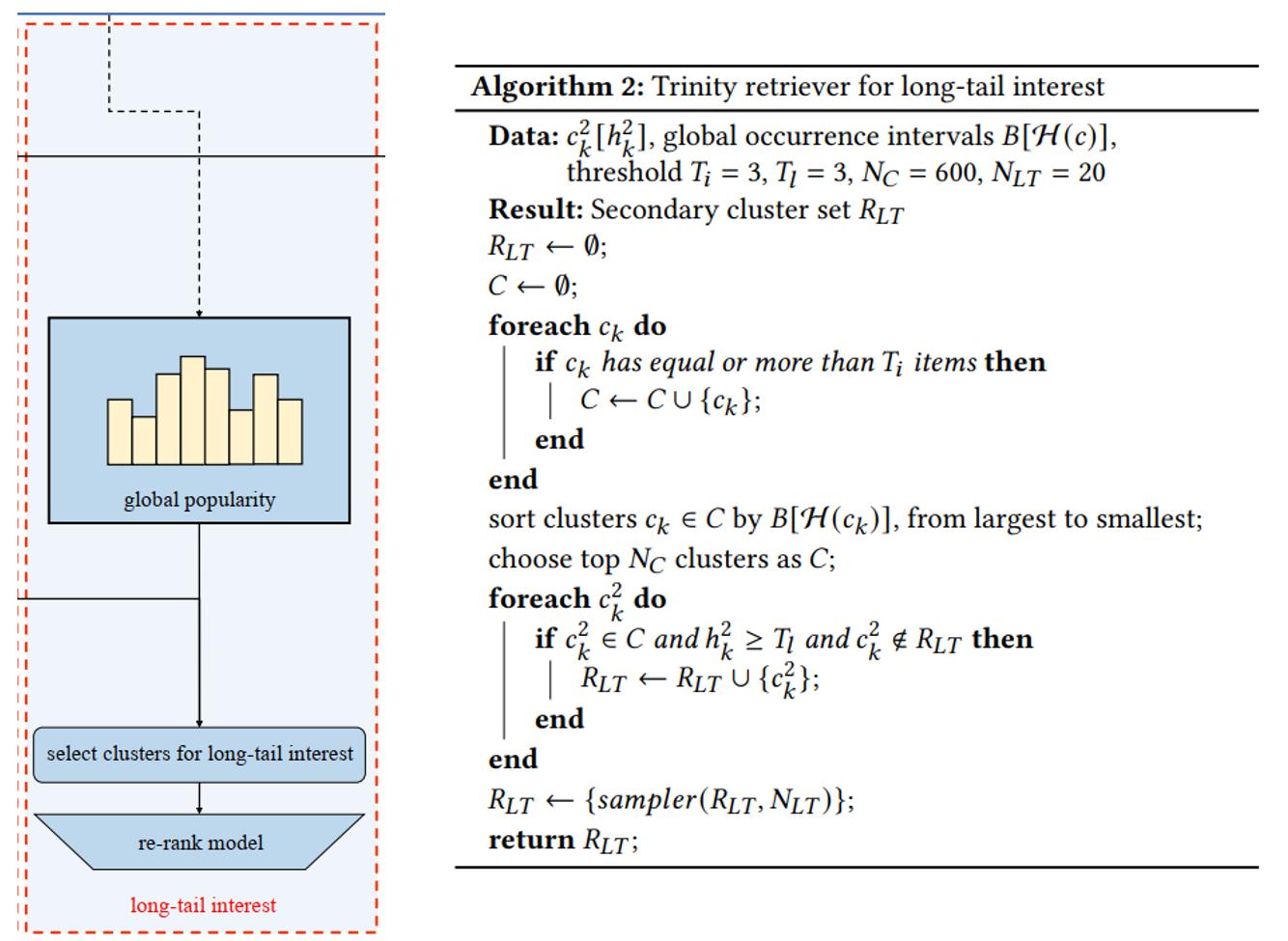
Long-term interest
最简单,直接用历史互动过或完播或播放时长>=10s的Item作为种子(当然,种子也需要模型进行排序),然后ANN(对每个Cluster被选取的Item数作限制)。
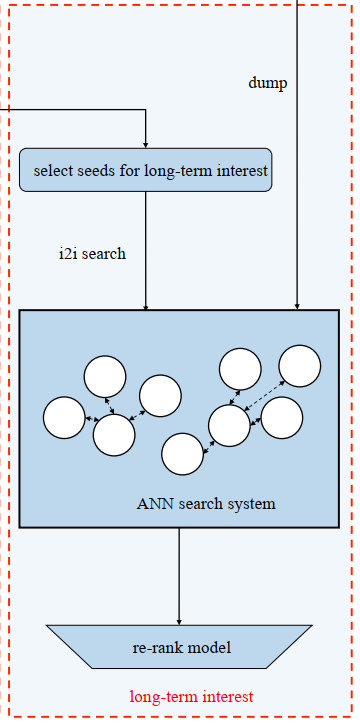
总的来看是用向量量化(VQ)生成动态标签,代替传统的静态标签,实现了对传统统计召回的升级。
Streaming VQ
VQ(Vector Quantisation),顾名思义是将一坨向量映射到一个索引,实际就是将向量分组。于推荐而言,召回中的VQ可以理解为由反向传播优化得到的动态分组方法。为什么召回需要分组,或者说需要索引?因为召回的候选是视频的全集,我们不可能在第一个阶段就对每个用户进行全候选计算,因此需要缩小范围。那么如何缩小范围?最简单的就是为用户以及视频打上标签,如我喜欢看日漫,那就只召回带日漫标签的。直接用标签分组缺乏灵活性,而VQ就是这么一个动态分组。
VQ-VAE
首先,VQ这种方式在Neurips2017的文章VQ-VAE中首次被用到了生成式任务中:
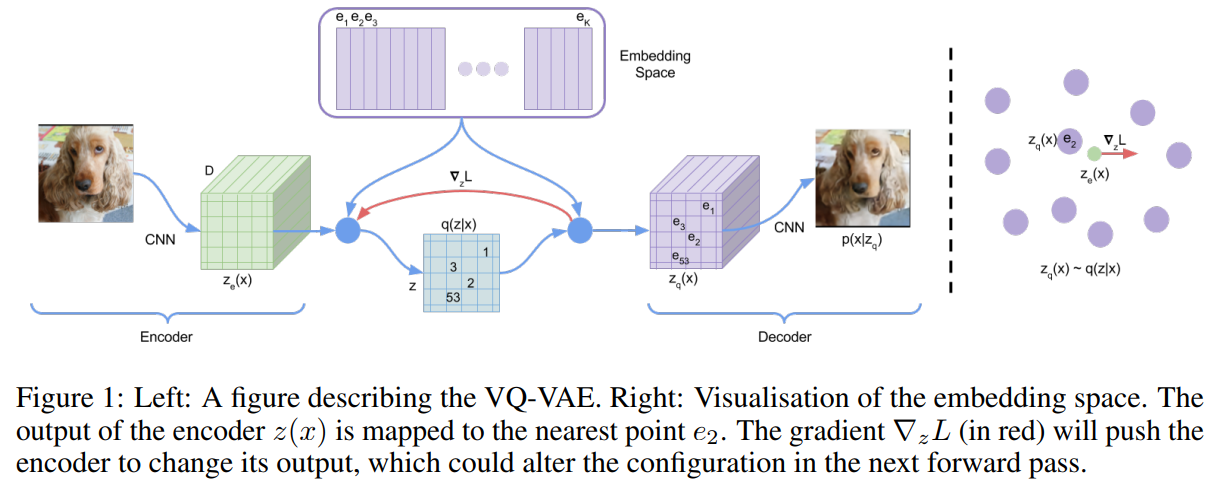
其对VAE Encoder的输出$z$进行了分组(后面都称索引),由于现实的图片分布可以理解为无数个高斯分布的叠加,因此这些索引我认为最终是实现了一个索引对应一个或者几个高斯分布。整个流程还是VAE那一套,量化体现在Encoder->Decoder的部分,即每个索引有其自身的Embedding,选取与Encoder输出欧式距离最近的组的Embedding作为Decoder的输入:
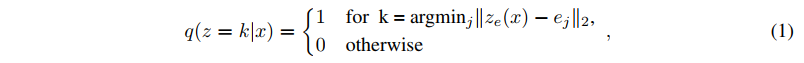
Loss由三部分组成(加号分割):
- $\mathcal{L} _1$即重构MSE,生成梯度用于更新Decoder,比较特别的是,由于输入Decoder的是索引Embedding,因此梯度不会传到到Encoder,作者的解决方式是:Decoder和Encoder的结构是一模一样的,因此直接用Decoder的梯度更新Encoder;
- $\mathcal{L} _2$中sg指stop gradient,用于更新索引Embedding。不难看出,最终每个索引的Embedding其实一定程度上等于该索引所包含的向量的均值,因此也可以采用指数移动平均EMA的更新方法,Streaming VQ用的就是这种方式;
- $\mathcal{L} _3$更新Encoder,起到正则的效果。
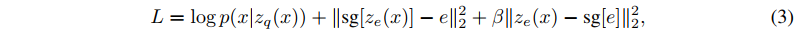
以上都是训练,实际Serving的时候就和VQ没什么关系了,还是从某个先验中采样出Embedding输入Decoder,而不是用Codebook(即索引表)的Embedding。
Streaming VQ
在VQ-VAE中,VQ实际上只是起到了一个辅助VAE训练的作用,最终的Codebook在Serving的时候并没有起到作用,而在Streaming VQ中,Codebook不仅有索引,每个索引下还有着对应的归属于该索引的视频,因而是有着实际作用的。
Training
整体架构如大的黑色虚线上面的部分所示:
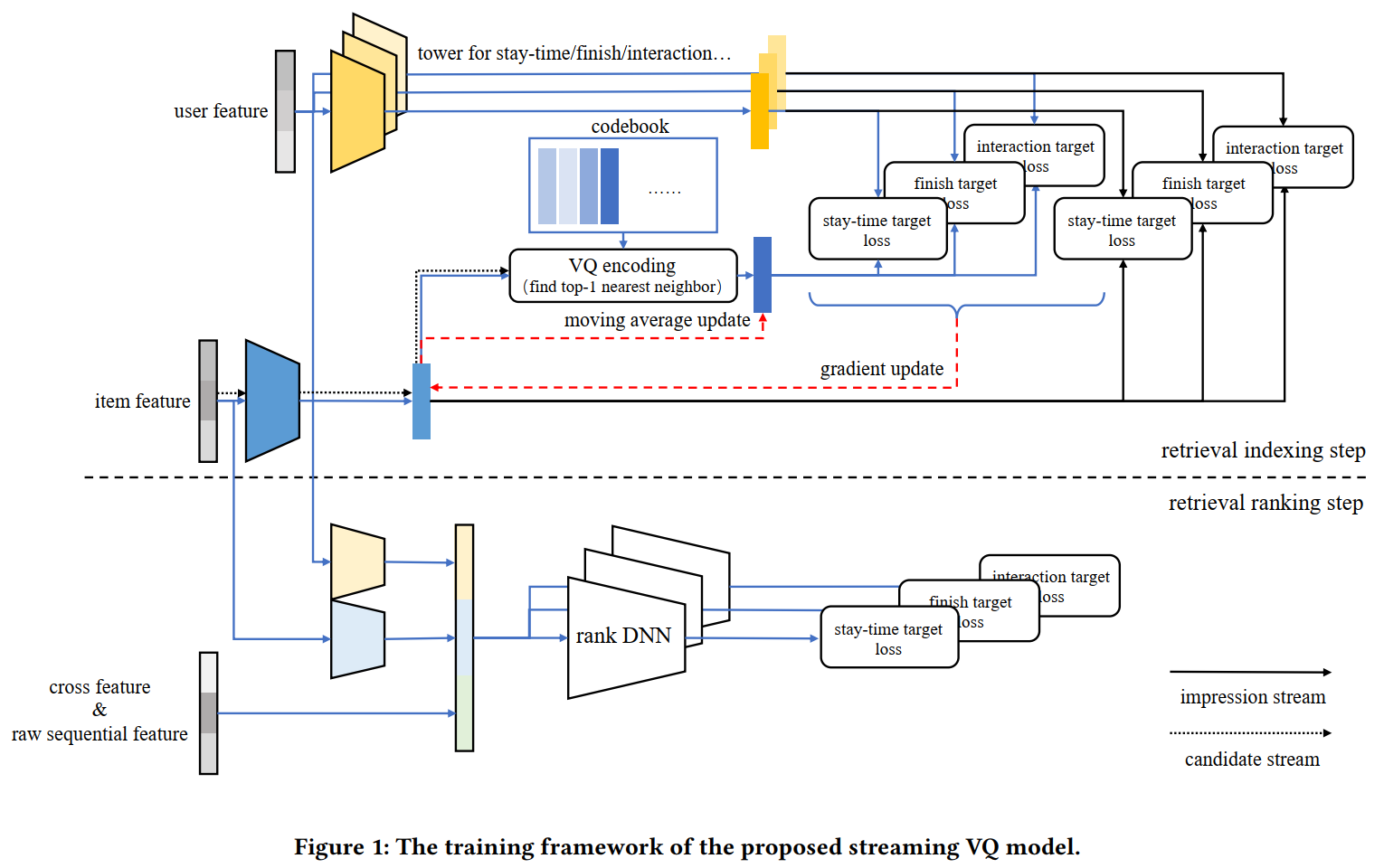
相比VQ-VAE,下游任务不再是重构,而是对应的推荐系统二分类任务,并且Codebook的更新使用了EMA,因此最终的损失函数实际只有一项,对应VQ-VAE的重构Loss,但细拆下来会有两项,分别是Item(视频)本身与User的分类Loss,以及Codebook与User的分类Loss:
Item_User:更新G侧和U侧。
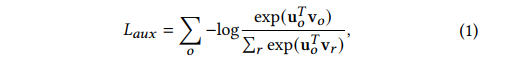
Fig. 5. Item-User
Codebook_User:Codebook的Loss回传更新G侧,Codebook本身由G侧Embedidng EMA更新,U侧是否更新不清楚。
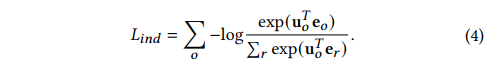
Fig. 6. Codebook-User
以上两者都采用In-batch softmax,即InfoNCE(无温度系数,定义见MoCo)。
In-batch softmax,本质上是一种负采样方法。对于一个Batch内的U-G对,将匹配的$U _i$与$G _i$作为正样本,而将$U _i$与$G _j$作为负样本,于是对一个大小为n的batch,就有n个正样本,n(n-1)个负样本。但这会导致视频成为负样本的概率与其出现次数成正比,导致对高热视频的打压,Sampling Bias即用于解决这个问题。
Serving
由于G侧塔和U侧塔的特征是完全独立的,因此在同一个时刻每个Item都会唯一地被分配一个索引,那么实际我们只要计算U侧Embedidng和Codebook各个索引Embedding的内积,取靠前的几个作为我们的候选即可。但是,用户的兴趣是多元的(或者说长尾的),分低的索引中也可能有用户很感兴趣的视频,前面的处理会导致过于注重头部兴趣,而忽略了尾部兴趣。Streaming VQ的解决方式是为每个Item引入单独的Bias项,起到Embedding表征个性化、Bias表征视频热门程度的作用:
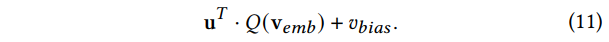
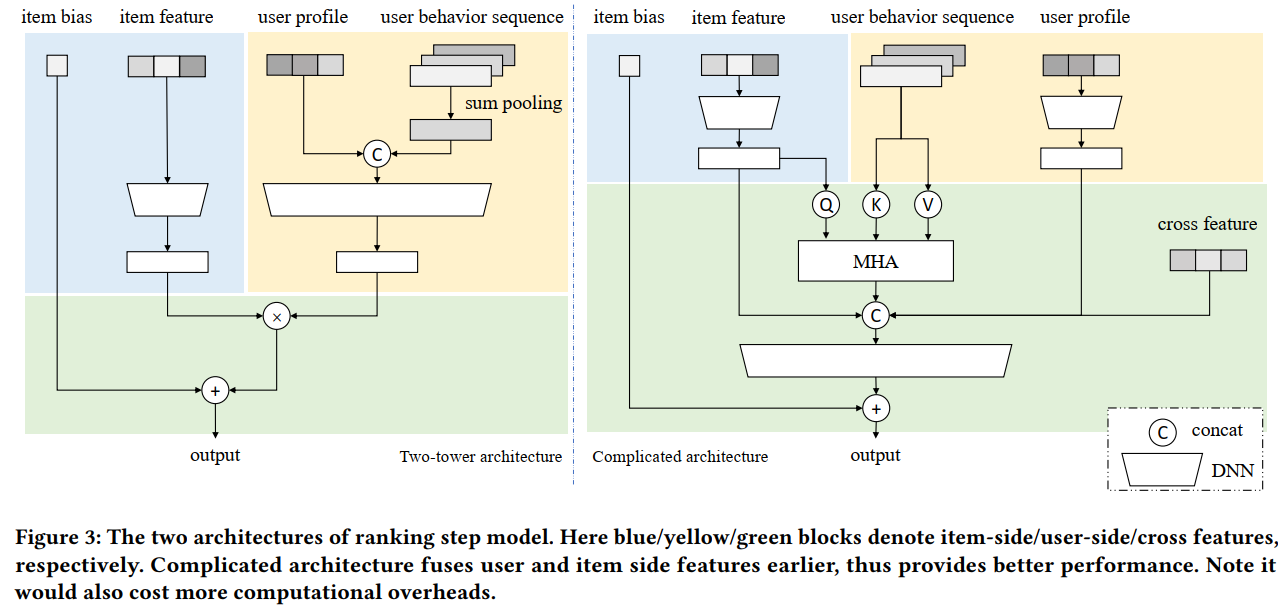
如此,Codebook中不同索引的Item也变得可比了,于是我们可以直接k路归并地召回:
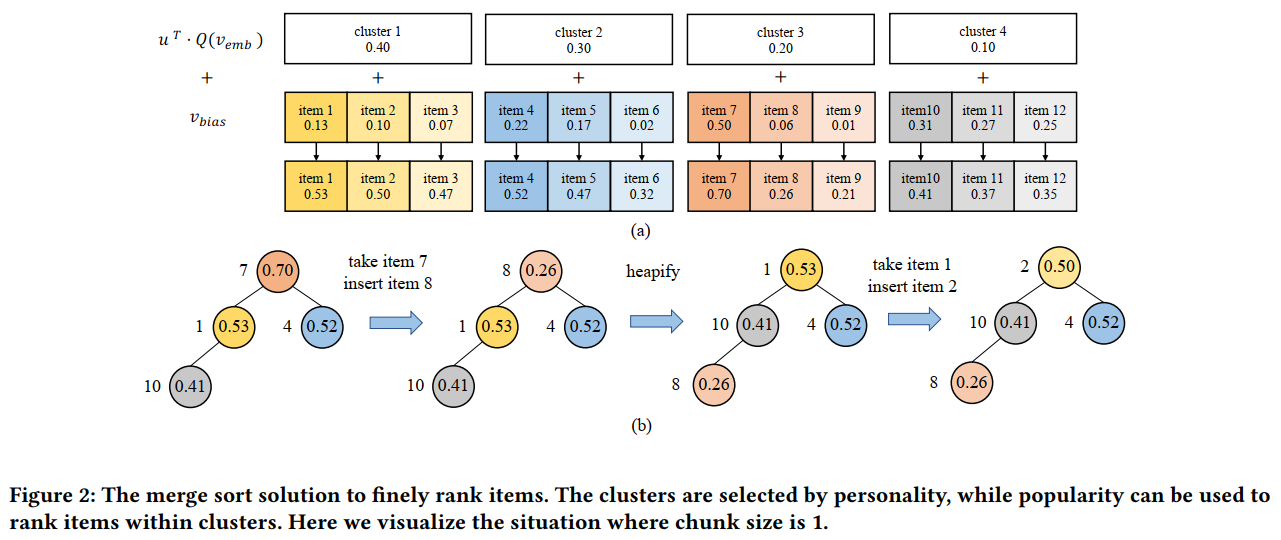
还有一个问题是,如何为所有的样本打上索引标签?文中的解决方式是两个数据流:
- 曝光样本组成的实时数据流:即正常的流式更新,有梯度回传,如Fig4中item feature的蓝线所示;
- 所有候选数据流:仅生成G侧塔的Embedding以及对应的索引,无梯度,如Fig4中item feture和黑色虚线所示。
Trick
总的框架就如上面所述,对一个用户,Serving时:User Embedding和Codebook Embedding内积求相似度->k路归并召回一定数量的视频->Ranking模型打分将前面的视频送入粗排。
但实际要真能在线上有用,还是需要一些小技巧。
Index Reparability
即视频对应索引的可变性。对比VQ-VAE和Streaming VQ的Loss可发现,除去Streaming VQ使用EMA代替梯度回传外,Streaming VQ还少了$\mathcal{L} _3$,即用于让Item Embedding不会过多偏移其所属的Codebook Embedding的L2正则项,起到的作用为让Item的对应的索引保持稳定。
如文中所述,图片的特征是静态的,其所属的索引保持稳定没有任何问题;而对于推荐的视频,其不少特征是动态变化的,如互动、播放量等,因此其对应的索引也应该是可变化的。故而Streaming VQ去掉了这一项正则,而让Item_User的Loss去更新Item。
Index Balancing
即每个索引包含的视频个数要尽可能地均衡。由于VQ的映射是多对一的,因此Codebook_User Loss这一项的存在会天然地要求每个索引所包含的视频个数尽可能一致,如5个视频5个索引,那肯定是一对一的Loss最小,因为这时Codebook Embedding就等于Item Embedding。
为了进一步提升均衡性,文中还有两个额外的改进:
- EMA时,用视频的在当前时间步的出现周期$\delta ^t$作为放缩项,减小高热Item的权重;同时维护一个索引k出现次数的计数$c _k$,打压高热Cluster的更新。
$$
\begin{align*}
\mathbf{w} ^{t+1} _k&=\alpha \mathbf{w} _k ^t+(1-\alpha)(\delta ^t) ^{\beta}v _j ^t,\\
c _k ^{t+ 1}&=\alpha c _k ^t+(1-\alpha)(\delta ^t) ^{\beta},\\
\mathbf{e} _k ^{t+1}&=\frac{\mathbf{w} _k ^{t+1}}{c _k ^{t+ 1}}
\end{align*}
$$ - 复用前面的$c _k$,对出现次数少的Cluster做一个Boost。
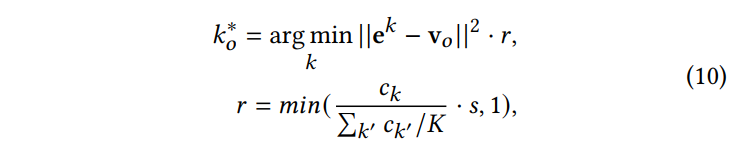
Fig. 10. Low loading cluster boost
即,在分布均匀可由VQ自身保证的情况下,分别从Item侧(防止Cluster被高热Item主导)和Cluster侧(防止训练被高热Cluster主导)做了平衡措施。
$\delta$定义源自Sampling Bias。按论文中的方法,为每个GID分配一个$\delta _i$,初始化为0,以及最近一次出现的epoch$t _i$,然后当其在本epoch出现时,移动平均地更新:$\delta _i=(1-\alpha) \delta _{i-1} + \alpha (t - t _i)$;$t _i = t$,不难看出,当更新步数足够大时,$\delta _i$即为对应视频出现的周期,那么$1/\delta _i$即为其出现的频率。原文用这个频率为In-batch softmax的双塔内积消偏,即:$s(x _i, y _j) - \log(p _j)$,最终效果为对热门物品,放大其打分。
Multi-task Streaming VQ
仅针对Indexing时的多目标,因为Ranking的多目标和粗精排没什么区别。
一言以蔽之:仅U侧塔个数变为多目标个数,前面的负载均衡公式引入每个目标的Reward项$h$(即0/1,是否为正样本,最终累乘的结果实际上就是一个多项式相乘的融分)调节多目标的更新权重:
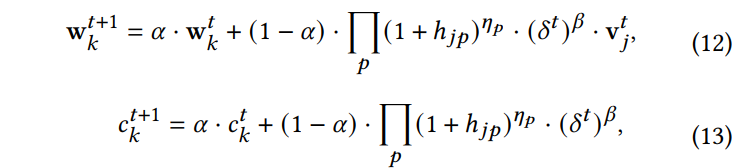
MERGE
MERGE从VQ索引的accuracy、uniformity以及separation,即:索引Embedding与内部物品Embedding相似度低、各索引大小不均以及索引Embedding间相似度过高这三个问题出发,构造了一个两级的、Codebook大小动态变化的、索引大小动态自平衡的生成式索引架构,最终用于替代Trinity的两级索引。
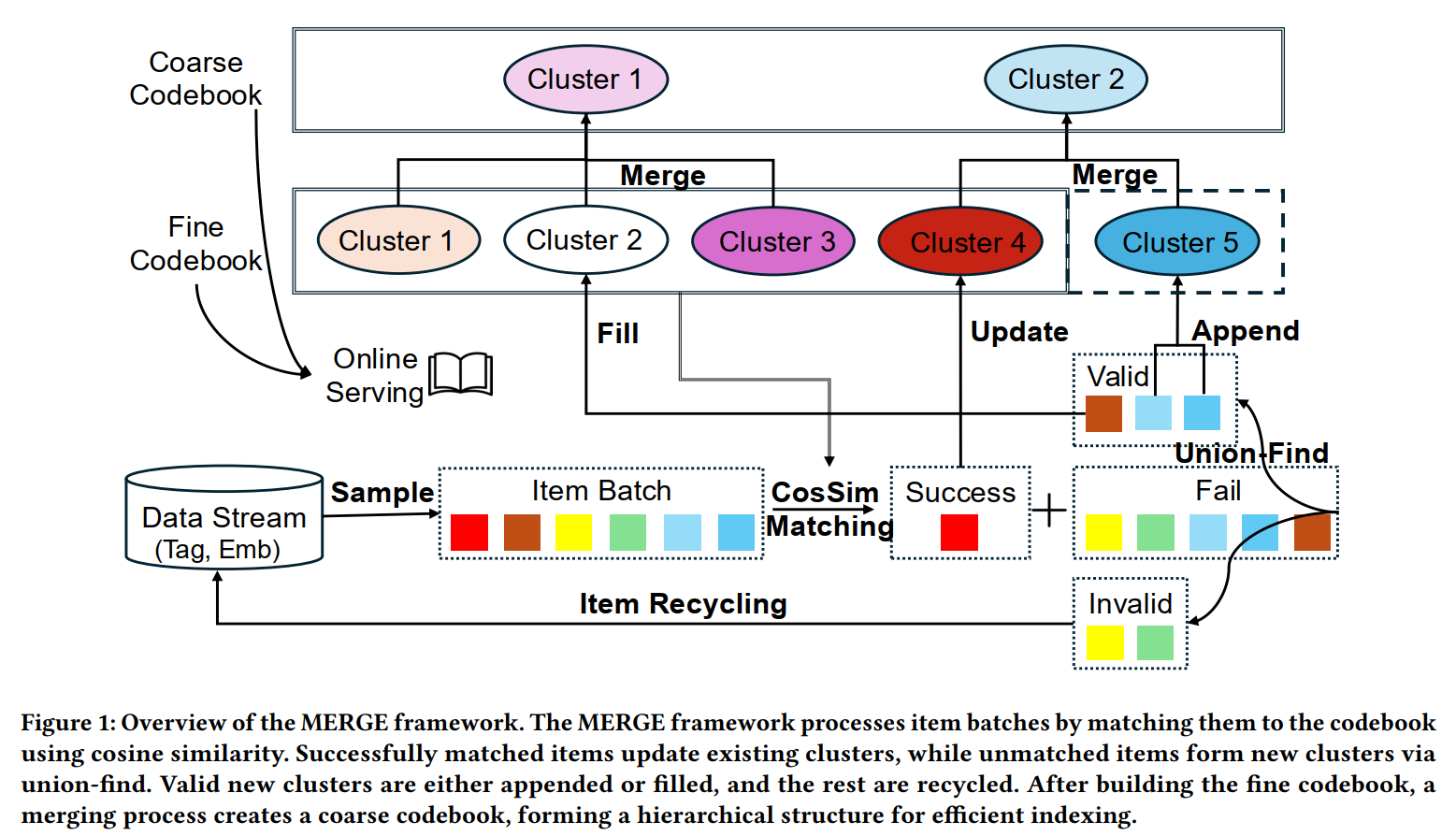
总体的流程可以从上图大致看出来,但还是简要概括一下:引入加入某索引的准入相似度$\tau$保证索引Embedding与内部物品Embedding的相似度、引入索引大小门槛$\epsilon _1$和$\epsilon _2$动态淘汰小索引、通过剪枝合并来保证一级索引间的差异性,具体而言:
- 各候选与索引计算相似度,得到各自的最大相似度$s _i ^*$与对应的索引$k _i ^*$;
- 对相似度大于阈值$s _i ^* > \tau$的候选,记为$\mathcal{B} ^+$,EMA更新索引Embedding$S _k$以及索引尺寸$N _k$,$q _k=\frac{S _k}{N _k}$作为归一化的最终索引Embedding:
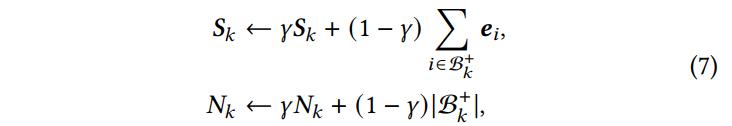
对这轮的Batch没有任何新物品进入的索引,不更新,因为其Embedding不会变,已有的归属也不会变,大小自然也不会变。
- 对相似度小于阈值的候选,记为$\mathcal{B} ^-$,计算这些候选间的相似度,大于阈值$\tau '$的之间连边,最终形成一张图,用Union-Find algorithm聚类,将size大于$m$的聚类形成新的索引或直接替换被淘汰的索引(淘汰规则见下),而经过这两轮筛选还没有进入任何索引的则直接进入下一轮的batch;
- 索引的淘汰由$\epsilon _1$和$\epsilon _2$两个阈值控制,underfilled直接淘汰,growing经过多轮仍未进入stable亦淘汰(淘汰即将索引Embedding置0,等待步骤3的索引将其替换);

- 剪枝聚类则是逐轮地将相似度最高的两个索引聚合为一个索引:
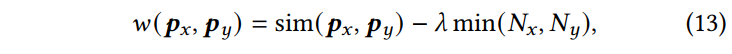
这样的方式确实会比Trinity直接训练两个大小不同的Codebook,以及RQ-VAE可能会导致误差积累的残差方式要更合乎逻辑,一是保证了一级索引内二级索引间的相似度,解释性更好;二是训练更加可控了。