Hyper Connections
以Transformer为根基的LLMs能发展至今,离不开Transformer设计的规整、对称性。对Transformer来说,经过Embedding层映射到向量空间的文本序列,成为了一个很规整的$T\times D$的矩阵,其中$T$是序列长度,$D$是Embedding维度。Attention生成动态权重进行序列维度的变换映射;FFN以固定的权重进行特征维度的变换映射,位置编码PositionEncoding赋予模型识别顺序、外延能力(当然Causal Attention本身就不具备置换不变性,内在地有顺序感知能力,但加上位置编码总归是更直接点),残差Residue以及正则Norm作为深度神经网络的基本组件保证训练的可持续与稳定性。
若再从Attention和FFN统一性的角度来看:Attention的QK内积生成权重,对V在序列维度加权求和;FFN(两层Linear维度分别为$D\times M$,$M\times D$)的输入与第一层Linear生成权重,对第二层的Linear在$M$维度加权求和。而稀疏性是普通存在的,因此很直接地,在FFN,对某个Token,在第二层的Linear中起到作用的肯定只有少数的行,因此有了MoE;同样地,与当前Token相关的历史Token也是少数的,即有用的V也就几个,因此有了稀疏注意力,如DSA。
对其他的组件,如PositionEncoding,从Sinusoidal到RoPE到YaRN等,一直在发展;Norm也由LayerNorm到RMSNorm(当然还有DyT)。现在终于轮到Residue以及TokenEmbedding了(悲QAQ)。本篇主要围绕字节的HC以及DeepSeek的mHC看看米娜桑都对残差整了些什么花活儿。
HC
emmm...怎么说呢,我十分认同openreview给5分的审稿人的意见,这篇文章的写作确实有点一言难尽。本来应该是很简单、直觉的方法,论文把它描述地过于复杂了,而且伪代码给得也不好。因此我决定跳过这篇文章,直接看mHC。
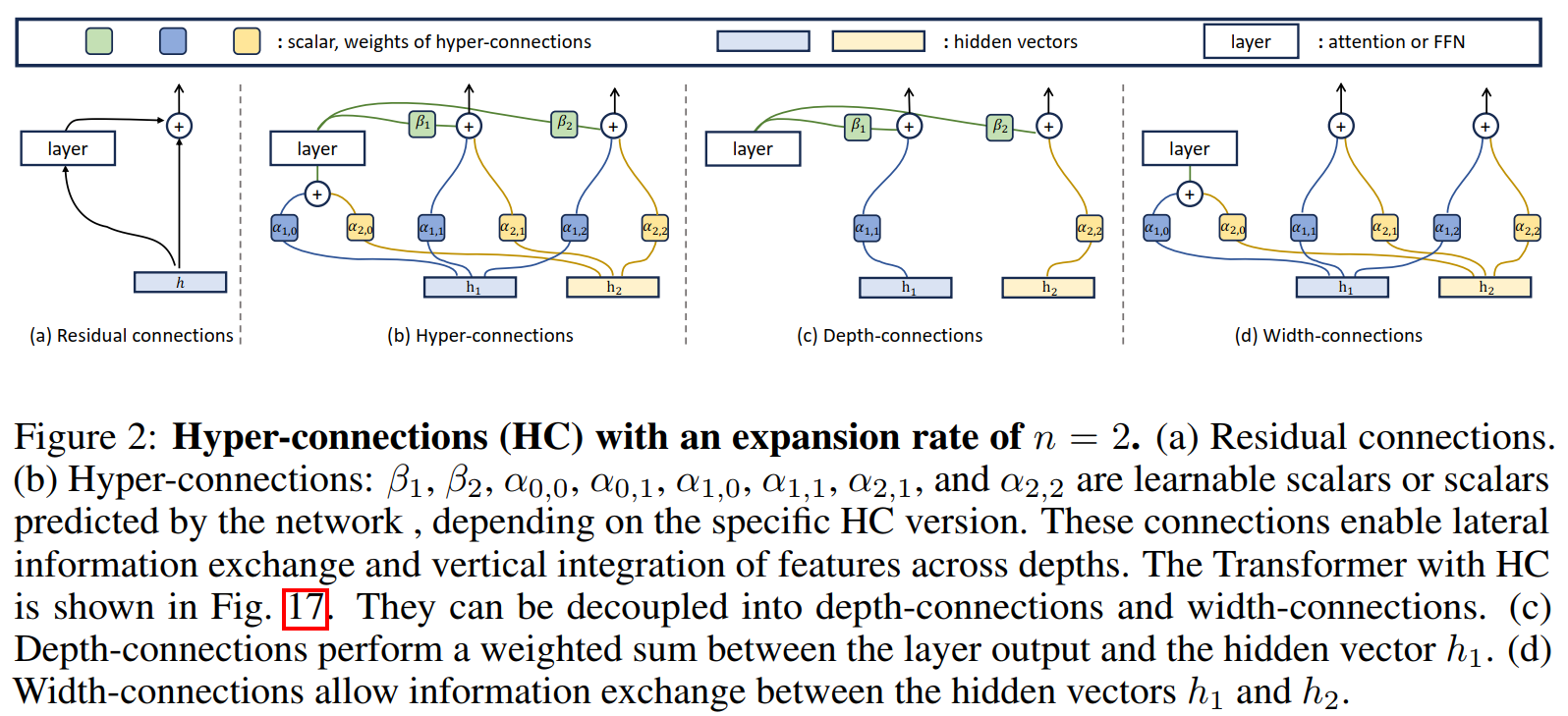
mHC
确实写得好不少,两个公式就概括了HC和普通的残差的区别,绘图也更为清晰:
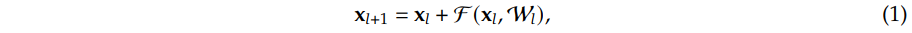
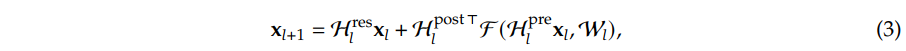
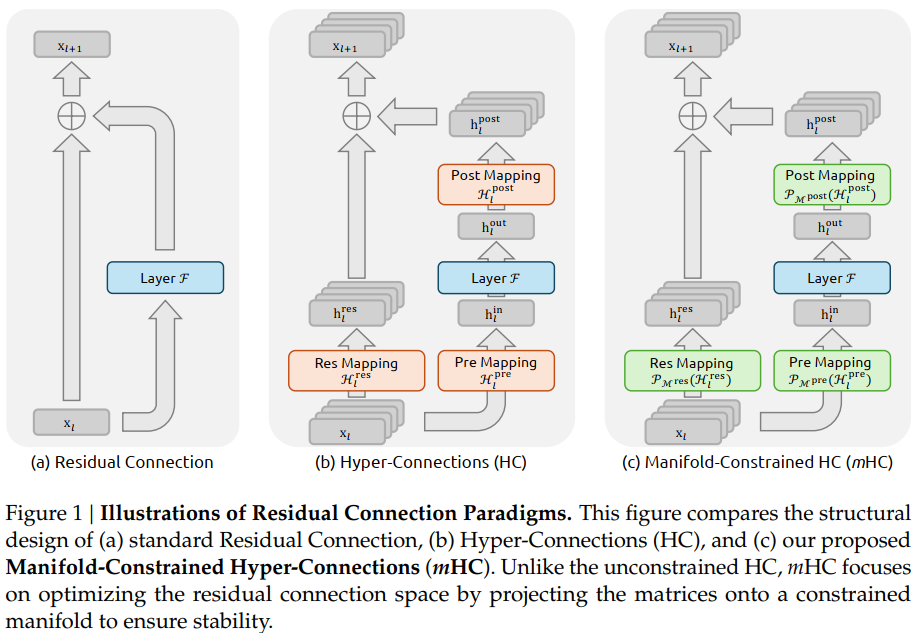
即相比于残差,HC人为地将恒等流由原来的一条增加为了n条,相应地输入$x _l$的维度也由$Batch\times SeqLen\times Dim$变为了$Batch\times SeqLen\times n\times Dim$(当然,在第一层的时候应该只是将原本的$x _l$复制了n份)。因此为了融合,会需要多个整合维度的投影矩阵,因此有了:$\mathcal{H} _l ^{pre}\in \mathbb{R} ^{n\times 1}$将输入的多流整合为一条流,输入Attention或FFN模块;$\mathcal{H} _l ^{post}\in \mathbb{R} ^{1\times n}$将Attention或FFN的输出重新转为n条流;$\mathcal{H} _l ^{res}\in \mathbb{R} ^{n\times n}$进行n条恒等流的交互。
然而,由于流信息交换矩阵$\mathcal{H} _l ^{res}$的存在(该矩阵也是HC收益的主要来源),原本不受层深度影响的恒等分支: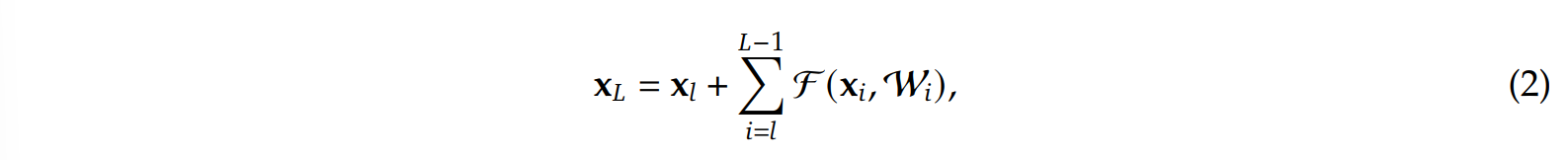
前面也多乘了一个$\mathcal{H} _l ^{res}$相关的累乘矩阵:
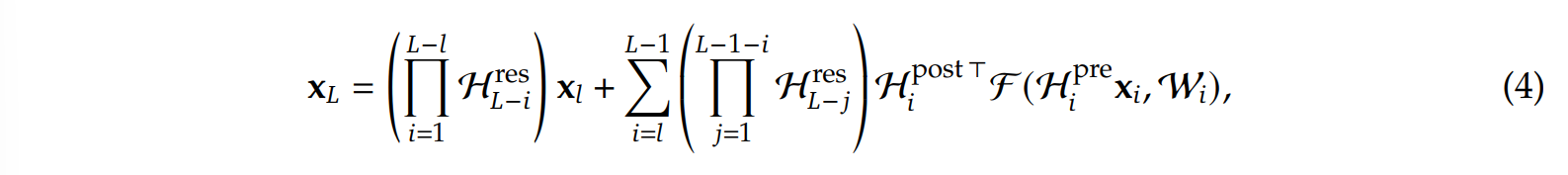
而$\mathcal{H} _l ^{res}$本身是不受任何限制的,因此可能会存在着梯度爆炸的问题(即原本只有一条流的时候始终加的是1,但现在多了个转换矩阵,最终的和可能 >> n)。mHC的主要改进点就是对上面的三个投影矩阵进行了值域限制。在HC中,三个投影矩阵的构造方式为:
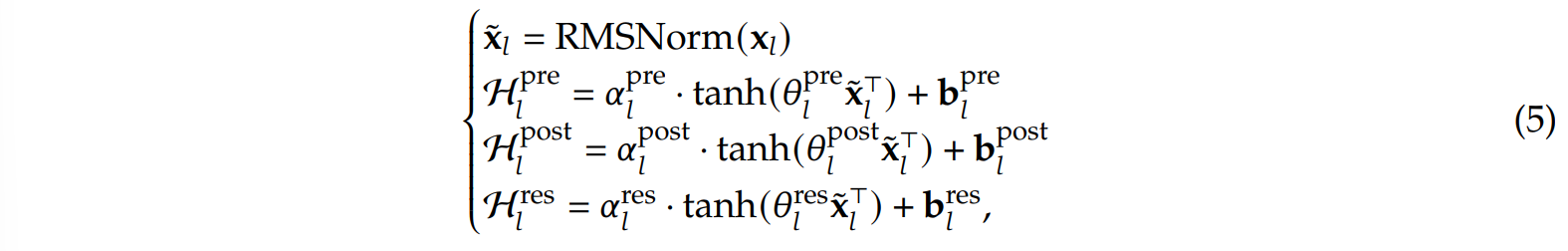
而在mHC中,除了去掉激活函数tanh,并将原本在投影时分开处理的n条流(维度$n\times Dim$)转变为在投影时共同处理的一条流(维度$1\times nDim$),强化了流之间的交互外: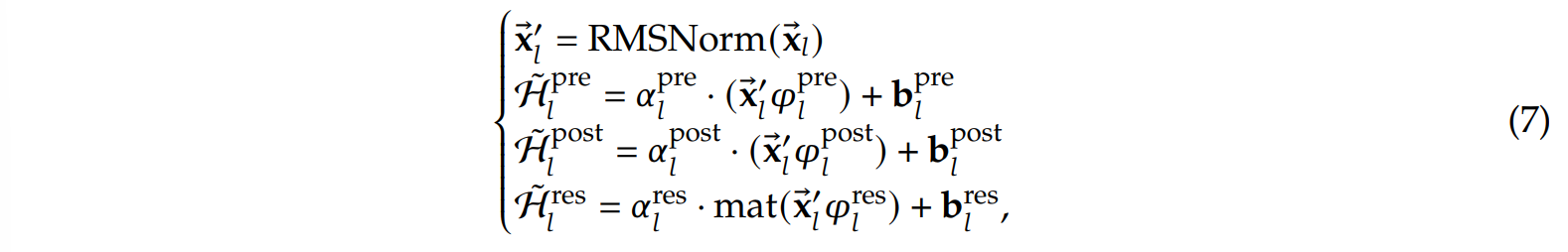
还对最终生成的转换矩阵进行了限制,其中前两个用sigmoid限制,最后的则用双随机矩阵限制,即要求行和、列和均为1且非负: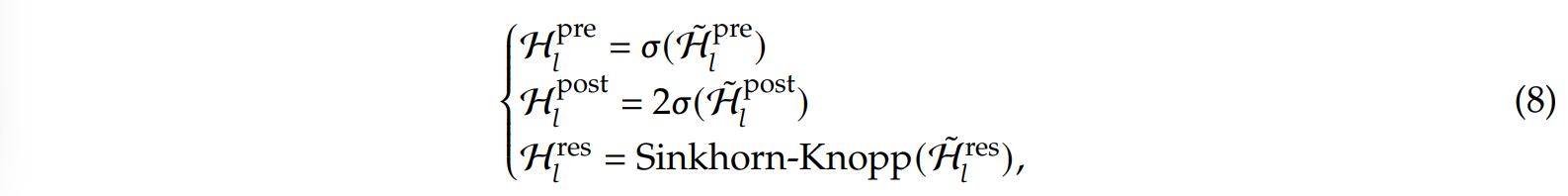
总结
通篇看下来感觉最强的还是后面的算子优化(虽然我也没细看,有需要再看),当然方法还是有较大的借鉴意义的。