PageRank

Posted on Edited on In Views: Word count in article: 2.3k Reading time ≈ 8 mins.
谷歌的搜索引擎发家算法--PageRank。虽然现在谷歌的搜索引擎中PageRank占比已经很少，但PageRank仍是一个重要的算法，且在与图相关的机器学习领域中继续发挥着余热，如APPNP就是用PageRank的衍生算法Topic-Sensitive PageRank优化了消息传递过程的图神经网络。

PageRank

PageRank将互联网视作由HTML网页组成的有向图（现在不行了，因为有许多不能被外部访问的内部网页，如朋友圈等），并为所有网页的重要性进行打分。当用户搜索相关网页时，PageRank便将得分高的网页放在搜索结果的前面。PageRank将任意互联网结点$i$的重要性定义为$r_i$，并将$i$的一条入度边视作另一个网页对$i$结点的引用，而将出度边视作$i$结点对其他网页的引用。PageRank的评分逻辑可以从三个角度进行理解。

解线性方程组

这是理解PageRank的第一个角度，也是最原理性的数学角度。一个很符合生活常识的逻辑是：某篇论文的重要性，不取决于这篇论文引用了什么论文，而是取决于哪些论文引用了这篇论文和这些引用了它的论文的重要性。对于互联网网页组成的图，也是如此。假设网页结点$j$的重要性为$r_j$，出度为$d_j$，其出度边平均地将$j$的重要性分给了它引用的网页，而$j$的重要性又是引用了$j$的网页分给$j$的重要性之和，则很自然地，$r_j$可以表示为：

$$
r_j=\frac{r_i}{3}+\frac{r_k}{4}
$$

1

Fig. 1. Rank of j

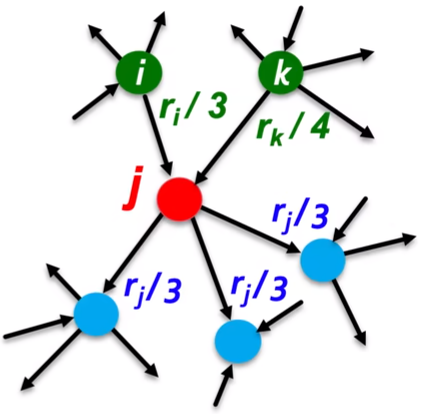
其中，3和4分别是$i$和$k$的出度。若将所有结点的重要性都用这种方式表示，我们便可以得到一个关于所有结点重要性的方程组：

$$
\begin{cases}
\vdots \\
r_j=\sum _{i\to j} \frac{r _i}{d _i}\tag{1}\\
\vdots
\end{cases}
$$

假设图的总结点数为$n$，那么这就是一个$n$元的线性方程组。我们有$n$个方程，然而实际有效的只有$n-1$个方程（很好理解，若$n$个方程都有效，我们将得到唯一解，但实际上将所有的$r$放大同样的倍数得到的值也是合理的），因此需要补充方程

$$
\sum _{i\in G}r_i=1
$$

以限制重要性的取值，其中$i\in G$指结点$i$是图中的结点。

以上便是PageRank的数学逻辑。若图的结点数量较少，我们可以用上面的联立方程组很快地得到解析解。但实际上$n$的值是十分大的，直接求解会很麻烦，因此只能采用近似的方法：假设每个结点的初始重要性都是$\frac{1}{n}$，将初始重要性代入式$(1)$中，可以得到更新后的重要性，这视作一次迭代。重复上述过程足够多次，所有结点的重要性都将收敛为一个稳定值。 这样的迭代是很合理的，因为所有网页诞生之初，其重要性都是一致的，只不过在后续网页间互相引用的过程中，其他网页为其引用的网页贡献了重要性，使得被引用的网页变得更加重要，而上述的迭代操作便是对这一过程的模拟。

矩阵形式的方程组

式$(1)$的方程组可以很容易地被转变为一个矩阵$\mathbf{M}$，其中：

$$
\mathbf{M} _{ji}=\frac{1}{d _i}
$$

表示结点$i$因为引用结点$j$而流向$j$的重要性占$i$自身重要性的比例。再令所有结点的初始重要性为向量$\mathbf{r}$：

$$
\mathbf{r}=[\frac{1}{n},...,\frac{1}{n}] _{1\times n} ^T
$$

于是，一次迭代便可视为$\mathbf{r}$左乘一次$\mathbf{M}$：

$$
\mathbf{r} ^{(k+1)}=\mathbf{M}\mathbf{r} ^{(k)}
$$

其中，$\mathbf{r} ^{(k)}$表示$\mathbf{r}$第$k$次迭代的结果。

矩阵$\mathbf{M}$又称Stochastic adjacency matrix（随机邻接矩阵），而这种迭代的方法称Power iteration（幂迭代）。从矩阵$\mathbf{M}$的名称不难看出其与邻接矩阵$A$具有不可分的关系，而这也是PageRank能被用于GNN的消息传递的原因之一（我猜的）。

当$k\to+\infty$时，$\mathbf{r}$将收敛为一个稳定的结果（事实上，$k$为50时就已经基本收敛）。计算机很擅长矩阵运算，因此这也是最常被用来计算PageRank的方法。

随机游走

另外一种理解角度是随机游走（Random walk）。假设图中有一个随机游走的surfer，在$t$时刻，它位于网页$i$；在$t+1$时刻，它将随机点击网页$i$中的超链接并到达网页$j$。初始时刻，surfer点击任何一个网页的概率相同：

$$
\mathbf{p}(0)=[\frac{1}{n},...,\frac{1}{n}] _{1\times n} ^T
$$

此后，每经过一次随机游走，surfer到达任意一个网页的概率都将发生变化：

$$
\mathbf{p}(t+1)=\mathbf{M}\mathbf{p}(t)
$$

此时，$\mathbf{M} _{ji}$可以视为从网页$i$跳到网页$j$的概率，$\mathbf{p}(t+1) _j$则是$t+1$次随机游走后，仍然在网页$j$的概率，其在数值上等于$t$次随机游走到达任意网页后又跳回网页$j$的数学期望。当$t\to +\infty$时，$\mathbf{p}(t)$便可被视为一开始surfer点击各个网页的概率向量（类似后验概率）。显然，概率越大的网页就越重要。

这是一种更加合乎人们上网习惯的模拟，也是更好理解的一种角度。

马尔科夫链

第三种角度是马尔可夫链，其定义的状态转移实际上可以看作一种随机游走，因此与第二种角度基本上是互通的。

Google Matrix

针对实际的网络，常规的$\mathbf{M}$并不是特别地好用，因为当图中包含以下这两类结点时，用$\mathbf{M}$计算得到的$\mathbf{r}$将失真：

  1. Dead ends

    此类结点只有入度，没有出度：

    2

    Fig. 2. Dead ends

    surfer一旦走入这类结点，将被永远地困在里面，导致重要性消失。

  2. Spider traps

    此类结点的唯一出度边是个自旋边：

    3

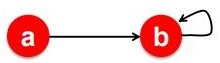
    Fig. 3. Spider traps

    Spider traps会导致所有的重要性被这一类结点吸收。

对于这两类结点，PageRank给出的解决方案是：1）Dead ends，人为地为其添加$n$条出度边，使其重要性能够流向所有的结点（包括自己）；2）Spider traps，在每一次迭代任意结点时，令其有$\beta$的概率按照原来的出度边流动，有$1-\beta$的概率随机流向所有结点（包括自己）的任意一个。于是，在处理完Dead ends后，一次迭代后$r_j$变为：

$$
\begin{align*}
r_j
&=\sum\limits _{i=0} ^{n-1} [\beta \mathbf{M} _{ji}+(1-\beta)\frac{1}{n}]r _i\\
&=\sum\limits _{i=0} ^{n-1} \beta \mathbf{M} _{ji}r _i+(1-\beta)\frac{1}{n}\tag{2}
\end{align*}
$$

上式成立因为$\sum\limits _{i=0} ^{n-1}r_i=1$。为了方便计算，PageRank定义了Google Matrix $\mathbf{G}$：

$$
\mathbf{G}=\beta\mathbf{M}+(1-\beta)[\frac{1}{n}] _{n\times n}
$$
$$
\begin{align*}
\mathbf{r} ^{(k+1)}
&=\mathbf{G}\mathbf{r} ^{(k)}\\
&=\beta\mathbf{M}\mathbf{r} ^{(k)}+(1-\beta)[\frac{1}{n}] _{n\times 1}\\
&=\beta\mathbf{M}\mathbf{r} ^{(k)}+(1-\beta)\mathbf{S}\tag{3}
\end{align*}
$$

从随机游走的角度，式$(2)$可视为人为地提高到达Non-spider traps结点的概率，使得surfer能够跳出Spider traps，但是仍保持总概率和为1。

Personalized PageRank

与PageRank是要计算图中所有结点的重要性不同，Personalized PageRank的目标是要计算所有结点与结点$j$的关联度。从随机游走的角度出发，我们就必须要让随机游走到达$j$的可能性最大，因为任何一个结点肯定与自身的关联性最大，由此，从$j$到达的结点分到的可能性也会增大，进而与$j$关联性大的结点就会被筛选出来。

要想达到这个目标，我们只能人为地引导surfer向$j$结点跳转，即，将式$(3)$中的$\mathbf{S}$更改为：

$$
\mathbf{S}=
\begin{cases}
\mathbf{S}_j=1\\
\mathbf{S}_i=0,i\ne j
\end{cases}
$$

使得任意结点不再是随机跳转到任意一个结点，而是随机跳转到指定结点$j$。

Personalized PageRank是PPNP（原始版的APPNP）的理论基础。

Topic-Sensitive PageRank

Topic-Sensitive PageRank可视为拓展版的Personalized PageRank。Topic-Sensitive PageRank的目标是基于用户的个人信息，为其提供更加个性化的搜索结果，如：当一个平时喜欢搜索篮球领域相关问题的人搜索“科比”时，搜索引擎便会为其提供更多有关篮球领域的“科比”而不是其他领域的“科比”的信息。

为达到这个目的，Topic-Sensitive PageRank也是在向量$\mathbf{S}$上做文章，不过它既不像PageRank那样广撒网，也不像Personalized PageRank“钟情于一人”，而是给予已知的拥有目标主题的网页更大的跳转机会，既：

$$
\mathbf{S}=\frac{[1,0,0,...,0,1,0] ^T}{\sum\limits _{i=0} ^{n-1}\mathbf{S} _i}
$$

Topic-Sensitive PageRank是APPNP的理论基础。

参考