Ridge Regression

Posted on Edited on Views: Word count in article: 2.4k Reading time ≈ 9 mins.
岭回归？L2正则！

向量求导

更确切地说是标量对向量求导，即，对：

$$
x\in\mathbb{R}^n,f:\mathbb{R}^{n}\to \mathbb{R}
$$

求标量$f(x)$对向量$x$的导数。与其一个个地展开，下列两个性质可以帮助我们快速地求解标量对向量的导数以及二阶导的海森矩阵：

  1. $\frac{\partial f(x)}{\partial v}=v^T\nabla f(x)$

其中$v$是方向向量，即$f(x)$对$v$的方向导数是$v^T\nabla f(x)$，这是很显然的，因为在二维的方向导数我们就有$\frac{\partial f}{\partial l}=f _x\cos \alpha+f _y \cos \beta$。推广到$n$维，$\cos\alpha...\cos\gamma$就是$v$的各个元素。

  • 例1：求$f(x)=x^T\mathbf{A}x$的梯度（$\mathbf{A}$是对称矩阵）：
    $$
    \begin{align*}
    \frac{\partial f(x)}{\partial v}=v^T\nabla f(x)
    &=\lim_{t\to 0}\frac{f(x+tv)-f(x)}{t} \\
    &=\lim_{t\to 0}\frac{(x+tv)^T\mathbf{A}(x+tv)-x^T\mathbf{A}x}{t}\\
    &=\lim_{t\to 0}\frac{tv^t\mathbf{A}x+x^T\mathbf{A}tv}{t}\\
    &=v^t\mathbf{A}x+x^T\mathbf{A}v\\
    &=2v^t\mathbf{A}x
    \end{align*}$$
    由于$v$的任意性，$\nabla f(x)=2\mathbf{A}x$
  • 例2：$f(\mathbf{\beta})=||\mathbf{X}\beta-y||^2$，求其对$\mathbf{\beta}$的梯度。
    $$
    \begin{align*}
    \frac{\partial f(\beta)}{\partial v}=v^T\nabla f(\beta)
    &=\lim_{t\to 0}\frac{f(\beta+tv)-f(\beta)}{t} \\
    &=\lim_{t\to 0}\frac{||\mathbf{X}(\beta+tv)-y||^2-||\mathbf{X}\beta-y||^2}{t}\\
    &=\lim_{t\to 0}\frac{||\mathbf{X}\beta-y+\mathbf{X}tv||^2-||\mathbf{X}\beta-y||^2}{t}\\
    &=\lim_{t\to 0}\frac{||\mathbf{X}tv||^2+2\sum((\mathbf{X}\beta-y)\odot (\mathbf{X}tv))}{t}\\
    &=2\sum((\mathbf{X}\beta-y)\odot (\mathbf{X}v))\\
    &=2(\mathbf{X}v)^T(\mathbf{X}\beta-y)\\
    &=2v^T\mathbf{X}^T(\mathbf{X}\beta-y)
    \end{align*}$$
    故$\nabla f(\beta)=2\mathbf{X}^T(\mathbf{X}\beta-y)$
  1. $\nabla ^2f(x)\cdot v=\frac{\partial \nabla f(x)}{\partial v}$

其中$\nabla ^2f(x)$是海森矩阵$\mathbf{H}$，$\mathbb{H} _{[i,j]}=\frac{\partial ^2 f}{\partial x _i \partial x_j}$。不难看出，$\nabla ^2f(x)\cdot v$是一个向量，其第$i$个元素为：$(\frac{\partial ^2 f}{\partial x _i \partial x_1},\frac{\partial ^2 f}{\partial x _i \partial x_2},...,\frac{\partial ^2 f}{\partial x _i \partial x_n})\cdot v$。

若令$g(x _i)=\frac{\partial f}{\partial x _i}$，则第$i$个元素实际上就是$\frac{\partial g(x _i)}{\partial v}$。

继续推广，令$g(x)=(\frac{\partial f}{\partial x _1},\frac{\partial f}{\partial x _2},...,\frac{\partial f}{\partial x _n})=\nabla f(x)$，则有$\nabla ^2f(x)\cdot v=\frac{\partial g(x)}{\partial v}=\frac{\partial \nabla f(x)}{\partial v}$。

  • 例3：求$f(x)=x^T\mathbf{A}x$的海森矩阵（$\mathbf{A}$是对称矩阵）：
    $$
    \begin{align*}
    \nabla ^2f(x)\cdot v=\frac{\partial \nabla f(x)}{\partial v}
    &=\lim_{t\to 0}\frac{\nabla f(x+tv)-\nabla f(x)}{t} \\
    &=\lim_{t\to 0}\frac{2\mathbf{A}(x+tv)-2\mathbf{A}x}{t}\\
    &=\lim_{t\to 0}\frac{2\mathbf{A}tv}{t}\\
    &=2\mathbf{A}v
    \end{align*}
    $$
    由于$v$的任意性，$\nabla ^2 f(x)=2\mathbf{A}$

矩阵求导

前面提到的向量求导的性质可以很容易地推广到矩阵求导（标量对矩阵求导），对：

$$
A\in\mathbb{R}^{n\times m},f:\mathbb{R}^{n\times m}\to \mathbb{R}
$$

有：

  1. $\frac{\partial f(\mathbf{A})}{\partial D}=< D,\nabla f(\mathbf{A}) >$
  2. $\nabla ^2f(\mathbf{A})\cdot D=\frac{\partial \nabla f(\mathbf{A})}{\partial D}$

其中，$D$是一个矩阵，$D\in \mathbb{R} ^{n\times m}$。由于内积是各元素相乘求和，故实际上$v^T\nabla f(x)$也可以表示为$< v, \nabla f(x)>$。性质$1$是显然的，只要把$D$拉伸为一个长$n\times m$的方向向量即可。

  • 例4：$f(\mathbf{A})=\text{tr}(\mathbf{AB})$，求其对$\mathbf{A}$的梯度。
    $$
    \begin{align*}
    \frac{\partial f(\mathbf{A})}{\partial D}=< D,\nabla f(\mathbf{A}) >
    &=\lim_{t\to 0}\frac{f(\mathbf{A}+tD)-f(\mathbf{A})}{t} \\
    &=\lim_{t\to 0}\frac{\text{tr}[(\mathbf{A}+tD)\mathbf{B}]-\text{tr}(\mathbf{AB})}{t}\\
    &=\lim_{t\to 0}\frac{\text{tr}(tD\mathbf{B})}{t}\\
    &=\text{tr}(D\mathbf{B})\\
    &=< D,\mathbf{B}^T >
    \end{align*}
    $$
    故$\nabla f(\mathbf{A})=\mathbf{B}^T$。最后的等式成立因为$\text{tr}(D\mathbf{B})=<D_1,{\mathbf{B} ^T} _1>+...+<D_m,{\mathbf{B} ^T} _m> =< D,\mathbf{B}^T >$，其中$D_i$表$D$的第$i$个行向量。

Ridge Regression：岭回归

岭回归（英文名：ridge regression, Tikhonov regularization）是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

共线性数据是指一些相互间存在比例关系的数据，这些数据的存在会导致输入参数$\mathbf{X}^T\mathbf{X}$的行列式为0，进而导致其不可逆。

例2中$f(\mathbf{\beta})=||\mathbf{X}\beta-y||^2$实际上就是对分类问题的最小二乘估计函数。令其对$\beta$的梯度为0，我们就可以得到参数$\beta$的精确值：

$$
\begin{align*}
\nabla f(\beta)=2&\mathbf{X}^T(\mathbf{X}\beta-y)=0\\\
&\downarrow\\
\hat{\beta}=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^Ty
\end{align*}
$$

但是，由于上面提到的问题，$(\mathbf{X}^T\mathbf{X})^{-1}$不一定存在，因而上述式子也就不一定成立，且仅仅一阶导为0我们不能判定此时的$\beta$就是极小值点。岭回归就是为了解决这一问题而提出的。对岭回归，有两种合理的解释，其中第一种从特征值的角度出发，第二种从惩罚项（正则）的角度出发。两种解释的结果是一样的，但是第二种解释与神经网络中的正则项联系更加紧密。

特征值角度

由：

$$
y^T\mathbf{X}^T\mathbf{X}y=(\mathbf{X}y)^T(\mathbf{X}y)\ge 0
$$

可知，$\mathbf{X}^T\mathbf{X}$是半正定矩阵，也就是说，其特征值$\lambda _i \ge 0$。要让$\mathbf{X}^T\mathbf{X}$可逆，我们只要使得其特征值$\lambda _i > 0$即可。故，我们将$\hat{\beta}$更改为：

$$
\hat{\beta}(k)=(\mathbf{X}^T\mathbf{X}+k\mathbf{I})^{-1}\mathbf{X}^Ty,\quad k>0\tag{1}
$$

由此，我们可以确保$\mathbf{X}^T\mathbf{X}$是正定矩阵，也就可以保证其可逆。

惩罚项角度

回到最小二乘函数$f(\mathbf{\beta})=||\mathbf{X}\beta-y||^2$，我们想从中确定一个$\hat{\beta}$，使得$f(\beta)$取最小值，即：

$$
\hat{\beta}=\text{arg}\min _{\beta}||\mathbf{X}\beta-y||^2
$$

使用原始式子我们可以得到：

$$
\hat{\beta}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^Ty
$$

而有些极端情况下$\mathbf{X}^T\mathbf{X}$的行列式即便不为0也是一个接近0的极小值。这将导致$(\mathbf{X}^T\mathbf{X})^{-1}$的行列式极大、内部元素的差异大，而这将间接地导致$\beta$数值的不稳定（这里面的关系不太懂）。为了限制$\beta$的波动，使其更稳定，我们需要对$\beta$的取值进行限制，即对其过大的取值进行一定程度的惩罚：

$$
\hat{\beta}=\text{arg}\min _{\beta}||\mathbf{X}\beta-y||^2+\lambda ||\beta||^2\tag{2}
$$

式$(2)$中新加入的项就是惩罚项，实际上就是深度学习中的L2正则项，对上式求导并令梯度为0可得：

$$
\begin{align*}
2\mathbf{X}^T(\mathbf{X}\beta-y)&+2\lambda \beta=0\\
\downarrow&\\
\hat{\beta}=(\mathbf{X}^T\mathbf{X}+&\lambda\mathbf{I}) ^{-1}\mathbf{X}^Ty\tag{3}
\end{align*}
$$

式$(3)$与式$(1)$完全一致。

极小值验证

进一步地，我们要验证$\hat{\beta}$就是极小值点，即我们要证明：

$$
\nabla ^2f(\beta)=\nabla ^2 (||\mathbf{X}\beta-y||^2+\lambda ||\beta||^2)
$$

是正定矩阵。这可以由向量求导的性质2得出：

$$
\begin{align*}
\nabla ^2f(\beta)\cdot v=\frac{\partial \nabla f(x)}{\partial v}
&=\frac{\partial 2\mathbf{X}^T(\mathbf{X}\beta-y)+2\lambda \beta}{\partial v} \\
&=\lim_{t\to 0}\frac{2\mathbf{X}^T(\mathbf{X}(\beta+tv)-y)+2\lambda (\beta+tv)-2\mathbf{X}^T(\mathbf{X}\beta-y)-2\lambda \beta}{t}\\
&=\lim_{t\to 0}\frac{2\mathbf{X}^T\mathbf{X}tv+2\lambda tv}{t}\\
&=2\mathbf{X}^T\mathbf{X}v+2\lambda v\\
&=(2\mathbf{X}^T\mathbf{X}+2\lambda\mathbf{I})v
\end{align*}
$$

即$\nabla ^2f(\beta)=2\mathbf{X}^T\mathbf{X}+2\lambda\mathbf{I}$，易知这是正定矩阵。所以$\hat{\beta}$就是我们要求的极小值点。

岭回归的收缩性

有定理能够证明：

$$
||\hat{\beta}(k)||\le ||\hat{\beta}||
$$

是严格成立的。事实上，岭回归的作用在于：保留蕴含信息量多的维度（参数），而剔除包含信息量较少的维度（参数）。这表现为某些不重要的参数$\beta _i$的数值接近0。

LASSO

LASSO采用的惩罚项是L1正则，即$\lambda \sum _{i=1} ^{p}|\beta _i|$。惩罚项的不同使得LASSO表现出与岭回归不同的性质，如：

  • LASSO会使得一些参数项变为0，让原参数向量变稀疏，而岭回归只会让参数向量收缩，并让一些接近0。

它们之间的区别可以用下面的图表示：

1

Fig. 1. Ridge Regression

2

Fig. 2. LASSO

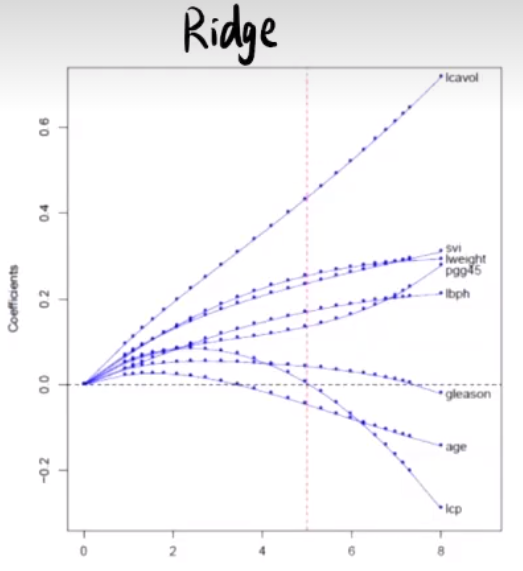
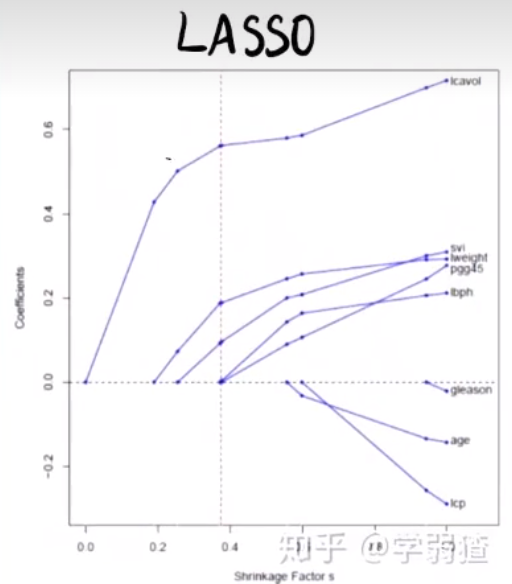
其中，上图为岭回归中的参数随$\lambda$的变化，下图为LASSO。横坐标均为$\lambda$，负轴方向为$\lambda$增大的方向。之所以会有这些的区别，是因为：若把岭回归和LASSO的最小二乘函数都视作拉格朗日函数，并将其惩罚项视作对$\beta$的约束条件，则其求解可转化为在约束条件下求$||\mathbf{X}\beta-y||^2$的最小值。最终的取值点表现为约束边界与$||\mathbf{X}\beta-y||^2$所确定等高线的切点：

3

Fig. 3. Lagrange

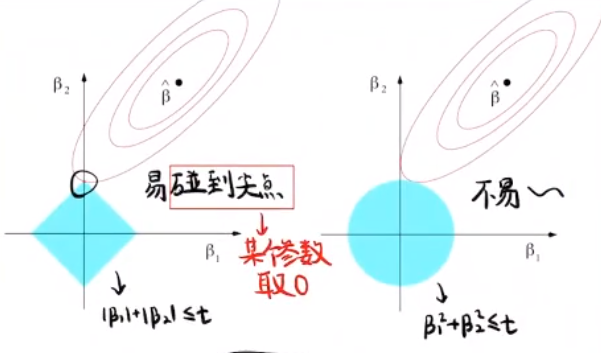
而由于LASSO约束边界的不光滑性，切点更容易落在让某个参数分量为0的尖点上。

参考