Position Embedding

Unlike RNNs, which recurrently process tokens of a sequence one by one, self-attention ditches sequential operations for parallel computation. To enable self-attention to perceive the sequence order, position embedding is a solution. The position embedding could either be learnable or fixed. Here we only consider the fixed position embedding.

Absolute Position Embedding

A typical kind of absolute position embedding is the sinusoidal function used in the vanilla transformer:

$$
\begin{cases}
p _{pos,2j}&=\sin(\frac{pos}{10000^{2j/d}}), \\
p _{pos,2j+1}&=\cos(\frac{pos}{10000^{2j/d}}),
\end{cases}
$$
where $pos$ is the position of token while $2j$ and $2j+1$ are embedding indices.

pe = torch.zeros(1, max_len, n_hiddens)
freqs = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1)
freqs /= torch.pow(10000, torch.arange(0, n_hiddens, 2, dtype=torch.float32) / n_hiddens)
pe[:, :, 0::2] = torch.sin(freqs)
pe[:, :, 1::2] = torch.cos(freqs)

• Bert, GPT2: Learnable Absolute PE
• Vanilla Transformer, GPT3: Sinusoidal PE

Relative Position Embedding

Unlike absolute position embedding, relative position embeddings focus on the relative position of query and key.

Generally, a query and a key with position embeddings could be formulated as:

$$
\begin{cases}
    \mathbf{q} _m=\mathbf{W} _q(x _m+p _m), \\
    \mathbf{k} _n=\mathbf{W} _k(x _n+p _n).
\end{cases}
$$

The resulting attention is:

$$
    \mathbf{q} _m ^T\mathbf{k} _n=x _m ^T\mathbf{W} _q ^T\mathbf{W} _kx _n+x _m ^T\mathbf{W} _q ^T\mathbf{W} _k p_n + p _m ^T\mathbf{W} _q ^T\mathbf{W} _k x_n + p _m ^T\mathbf{W} _q ^T\mathbf{W} _k p_n.
$$

The relative position embedding only needs to replace $p _m$ and $p _n$ with the relative forms. The simplest one is:

$$
    \mathbf{q} _m ^T\mathbf{k} _n=x _m ^T\mathbf{W} _q ^T\mathbf{W} _kx _n+x _m ^T\mathbf{W} _q ^T\mathbf{W} _k p _{m-n} + p _{m-n} ^T\mathbf{W} _q ^T\mathbf{W} _k x_n
$$

Relative position embedding are typically encoded as biases and added to attention scores (not to values). Another difference between relative and absolute position embedding is that relative position embedding is applied to each layer while absolute position embedding is only added in the bottom layer.

Rotary Position Embedding

The intuition of RoPE is that the vanilla Add PE not only change the magnitude but also change the radius, which will cause the position embedding to change irregularly, resulting in the model only being able to memorize the data but not actually learn the position. This in turn causes the model to be unable to extend to positions that have not been seen in the training set.

RoPE uses the rotation matrix of the two-dimensional vector space so that the same token at different positions only changes in angle. That is:

$$
    \mathbf{q} _m ^T\mathbf{k} _n=(\mathbf{R} ^d _{\theta, m}\mathbf{W} _qx _m) ^T(\mathbf{R} ^d _{\theta, n}\mathbf{W} _kx _n)=x _m ^T\mathbf{W} _q ^T\mathbf{R} _{\theta, n-m} ^d \mathbf{W} _k x _n
$$
where

$$
\mathbf{R} _{\theta, m}=\begin{pmatrix}
&\cos m\theta _1 &-\sin m\theta _1 &0 &0 &\cdots &0 &0\\
&\sin m\theta _1 &\cos m\theta _1 &0 &0 &\cdots &0 &0\\
&0 &0 &\cos m\theta _2 &-\sin m\theta _2 &\cdots &0 &0\\
&0 &0 &\sin m\theta _2 &\cos m\theta _2 &\cdots &0 &0\\
&\vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots\\
&0 &0 &0 &0 &\cdots &\cos m\theta _{d/2} &-\sin m\theta _{d/2}\\
&0 &0 &0 &0 &\cdots &\sin m\theta _{d/2} &\cos m\theta _{d/2}\\
\end{pmatrix}
$$
is the rotary matrix with the same $\theta _i$ as the sinusoidal function. Intuitively, the rotation matrix is ​​realized by grouping the embedding dimensions in pairs to expand the two-dimensional rotation matrix to multiple dimensions.

Fig. 1. Vanilla PE (left) and RoPE (right)

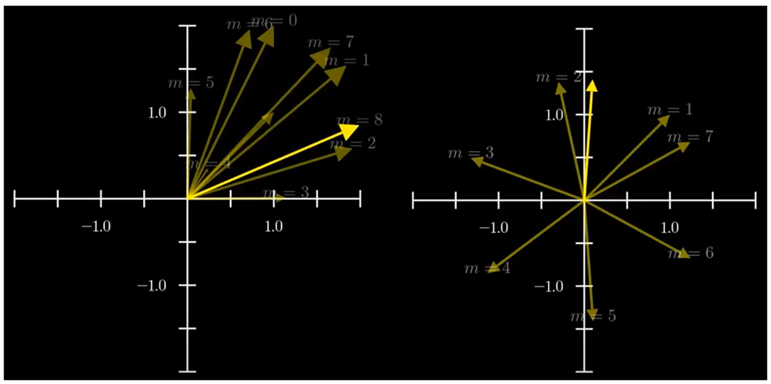
Compared with the vanilla position embeddings, RoPE has several advantages:

1. Incorporating relative position information more efficiently.
2. Long-term decay: the attention weight will decay when the relative position increases.

Adopted by:

• Llama
• GPT3.5, GPT4, GPT4o

Fast Calculation

Actually, in the two-dimensional case, $\mathbf{R} _\theta x$ ($x=(x _1, x _2)$) can be converted to complex number calculation, that is:

$$
\mathbf{R} _\theta x=(\cos\theta + i\sin\theta)(x _1+ix _2)=(\cos\theta x _1-\sin\theta x _2) + i(\sin\theta x _1 + \cos\theta x _2)
$$

whose coeffiencts are the result. The following is a quick start (from Llama):

def precompute_freqs_cis(n_hiddens: int, max_len: int, base: float = 10000.0):
    """
    Turn R_{\theta,m} into complex form 
    """
    pos = torch.arange(max_len, dtype=torch.float32)
    freqs = 1.0 / torch.pow(base, torch.arange(0, n_hiddens, 2, dtype=torch.float32) / n_hiddens)
    # outer product, shape [max_len, n_hiddens//2]
    freqs = torch.outer(pos, freqs)
    # complex 64, shape, shape [max_len, n_hiddens//2]
    freqs_cis = torch.polar(torch.ones_like(freqs, freqs))

    return freqs_cis

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    """
    freqs_cis: [max_len, n_hiddens//2] (complex)
    x: [batch, max_len, n_hiddens//2] or [..., max_len, n_hiddens//2] (complex)
    """
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]

    return freqs_cis.view(*shape)

def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
)
    """
    Assume xq and xk: [batch, max_len, n_hiddens]
    freqs_cis: [max_len, n_hiddens//2] (complex)
    """
    # [batch, max_len, n_hiddens] -> [batch, max_len, n_hiddens//2] (complex)
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    # [max_len, n_hiddens//2] -> [1, max_len, n_hiddens//2] (complex)
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    # [batch, max_len, n_hiddens//2] (complex) -> [batch, max_len, n_hiddens//2, 2] -> [batch, max_len, n_hiddens]
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)

    return xq_out.type_as(xq), xk_out.type_as(xk)

ALiBi

ALiBi

CoPE

CoPE

No Position Embedding

NoPE means training transformers without position embedding. It can only apply for decoder-only structure (GPT, Llama), but not encoder-only structure (Bert). The reason might be that the causal attention in autoregressive transformer language models allows them to predict the number of attendable tokens at each position, i.e. the number of tokens in the sequence that precede the current one .